密码学基础

Created2021-08-14Updated2022-03-22

第二章 古典密码

1.Monoalphabetic Cipher:

单字母替代密码(将明文字符集和密文字符集建立映射关系)

▲单表替代：明文字符集与密文字符集任意替代(一一映射)，那么n个元素即有n!种置换。(若仅仅针对字符集，那么可以通过字母的使用频率来分析解密)

(1)Caesar密码：

将字母用它之后的第三个字母进行替代(26个字母循环)

(2)keyword密码：

  • key：随意选取一个关键词key

  • 去重：将key中的重复字母去掉，例如：success->suce

  • 填表：将去重的key填入26个字母表前面位置，依次序接着填满26个字母。

1
2
3
4
//注释头

suceabdfghijklmnopqrtvwxyz
abcdefghijklmnopqrstuvwxyz
  • 加密：依据上表，查表将明文替代为密文。

(3)Multiliteral Cipher：

随意选取一个五字母的关键词key

  • 填表：依据关键词key形成5×5的矩阵，将26个字母填充进去，其中i/j为一个。

  • 加密：每个字母直接转换为key的行和列，即一个字母直接变成两个字母。

(比较脆弱，因为密钥就存在于密文中)

☆分析：利用字母使用频率分析：

img

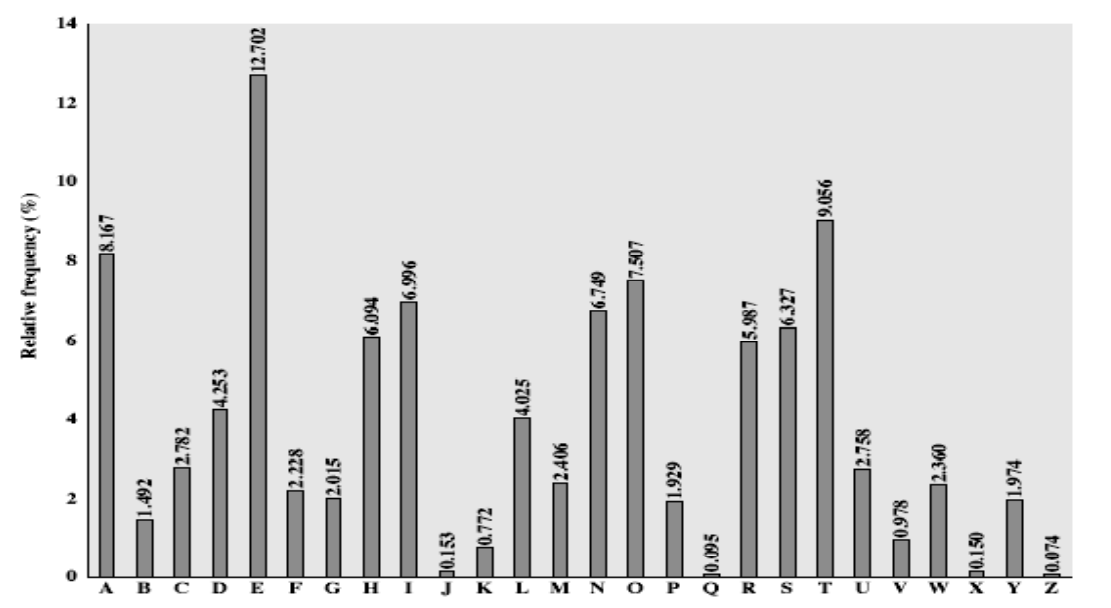
2.Polyalphabotic Cipher：

多表替代密码，减少字母频率特征

(1) Vigenere Cipher：

  • key：随意选取一个关键词key

  • 对应：

1
2
3
4
//注释头

HOLD HO LDH OLDHOLDHO
THIS IS THE PLAINTEXT

  • 加密：

    • 查表加密(行列查表都可以，因为对称的)：

      img

    • mod26加密：

1
2
3
4
5
6
7
8
9
10
11
12
//注释头

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A B C D E F G H I J K  L  M  N  O  P  Q  R  S  T  U  V  W  X  Y  Z

            7  14 11 3  7  14 11 3  7  14 11 3  7  14 11 3  7  14
key:        H  O  L  D  H  O  L  D  H  O  L  D  H  O  L  D  H  O 
plaintext:  T  H  I  S  I  S  T  H  E  P  L  A  I  N  T  E  X  T
            19 7  8  18 8  18 19 7  4  15 11 0  8  13 19 4  23 19

相加mod26：  0  21 19 21 15 6  4  10 11 3  22 3  15 1  4  7  4  7
ciphertext: A  V  T  V  P  G  E  K  L  D  W  D  P  B  E  H  E  H

以上两种方法都可以。

☆分析：

  • 算密钥长度：一段密文中查找重复出现的几个字节，计算重复出现的几个
1
2
3
4
5
//注释头

key:        R U N R U N R U N R U N R U N R U N R U N R U N R U N
plaintext:  T O B E O R N O T T O B E T H A T I S T H E Q U E S T
ciphertext: K I O V I E E I G K I O V N U R N V J N U V K H V M G

KIOV和下一个KIVO，NU和下一个NU，分别相差9个字母，6个字母，多次重复计算，算出公因数，这里公因数是3，那么3就可能是密钥长度。

  • 变成单表替代：假设得到公因数长度为abcdef，则进行如下计算：
1
2
3
4
//注释头

key:        abcde fabcd efabc defab cdefa bcdef abcde fabcd efabc defab
ciphertext: lpkso fjbnn mpfls rneoi yqrlx bkqtz ucxot ssbvb wpjil geckb

将所有由a加密的字母提取出来，为 ljfoxusjk…….重复多次。(这里选取abcdef中任意一个都可)。转换成6个单表替代密码，之后即可从单表替代密码ljfoxusjk…….中进行字母频率分析，逐步破译。(比如说j就有可能是e)

(2)Autokey Cipher(针对Vigenere Cipher的改进)：

选取关键词

  • key：选取关键词Key

  • 初次：key加密对应数量的密文

  • 重复：将前一次加密得到的密文拿来作为key加密。

☆很脆弱，密文即为密钥的一部分，可通过错位分析来直接解密：

1
2
3
4
5
//注释头

key:         capcnpwgd
plaintext:   anautokeycipherprovidesalongkeyword
ciphertext:  cnpwgd...........................

初始密钥为cap，之后依次得到cnp，wgd….

(3)AutoKey Plaintext：

(类似，但是是拿明文再进行加密)

3.Rotor Ciphers：

转轮密码

  • 轮子的内部对应关系不变，外在触点可以转动：

img img

  • 利用多个轮子合在一起形成加密关系，转动触点即可改变加密关系：

img img

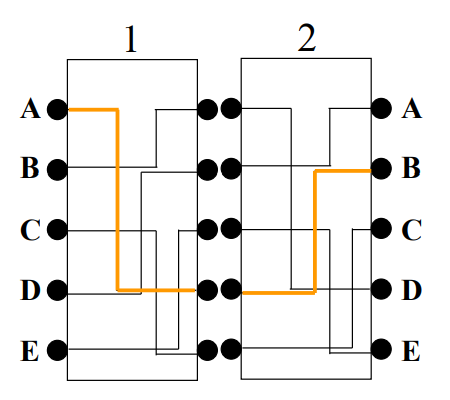
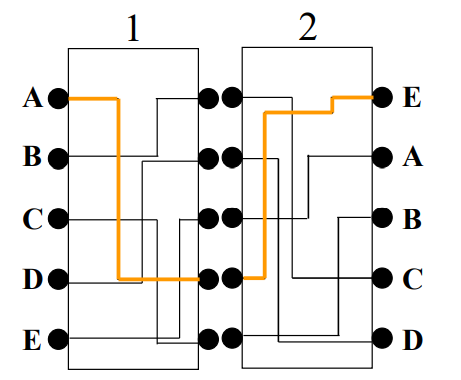
这里的初始化状态和转动方式就可看作是密钥。

4.Polygraphic Cipher：

多图替代密码

(1)Play fair密码：

双字母音节替代加密

  • key：随意选取密钥key

  • 填表：key顺序加上剩余字母依次排列进5×5表中(这里key为harpsichord)

img

  • 分组：对明文进行按两个字母一对进行分组，如果其中有字母对两个字母相同，就在其中填充一个其他字母(这个字母最好选取出现概率较小的字母，比如xx基本不会出现)：ballon -> ba lx lo on

  • 加密：

    • 落在矩阵同一行的明文字母对中字母由其右边字母代替，最右边则由最左边替代。例如：AR->RP
    • 落在矩阵同一列的明文字母对中字母由其下边字母代替，最下面则由最上面替代。例如：IM->EV
    • 不同行不同列的则由对称行列转化加密(同行替换)，例如：CT->DN，OU->BQ….

☆分析：(m1,m2)->(c1,c2)，那么如果有(m2,m1)，则一定是(m1,m2)->(c2,c1)。可以将明文和密文对比移位。(具体的看PDF)

(2)Double playfair密码：

  • 选取两个关键词key，去重，填表构建两个矩阵，行对应排列：

img

  • 给定一个数字，所有明文按照所选数字分组进行排列，不足的补指定字母。例如给定明文为this is double playfair cipher，数字为10，不足补x：
1
2
3
4
5
6
7
#注释头

thisisdoub
leplayfair

cipherxxxx
xxxxxxxxxx

  • 按组进行加密，上述分组情况即为tl,he,ip…..cx,ix,px…….xx共计20组。

  • 对每组进行加密，分别从两个矩阵中找到明文字母对，加密规则类似：

    • 不同行的即对角线交换：tl->op
    • 同行的由右边字母替代，但这里替代完之后还需要交换一下：br->ac

5.Transposition cipher：

(1)Skytale cipher：

缠绕密码，一张图说明一切

img

(2)Permutation cipher：

  • 给定密钥，按字母表排列顺序。例如key，顺序为(2 1 3)。

  • 依据密钥长度分组明文，不足补指定字符。例如Permutation cipher，分为Per mut ati onc iph erx(最后补了x)

  • 根据密钥顺序置换，(2 1 3)即代表第二个字母放到第一个，第一个字母放到第二个，第三个字母放到第三个。可得ePr umt tai noc pih rex即为所求密文。

(3)Column Permutation cipher：

  • 给定密钥，按字母表排列顺序。例如key，顺序为(2 1 3)。

  • 依据密钥长度分组明文，竖向排列。例如Permutation cipher，分为

1
2
3
4
5
6
7
8
9
#注释头

213
Per 
mut 
ati 
onc 
iph 
er
  • 依据顺序将列竖向提取，横向生成密文：eutnpr Pmaonie rtich即为所求密文。

(4)Double Permutation cipher：

一样，只是重复两次

第三章 流密码

Stream Cipher 生成

1.LFSR：

给定初始值，指定反馈位异或生成从左边进入，从右边出来生成生成密钥流，这里就会是101011 00….

img

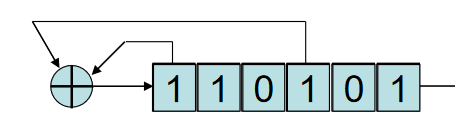
☆针对LFSR攻击：将密文逐两个异或得到分析段，如图第一段为密文段，第二段为分析段，其中重复部分相距的长度即为LFSR的两个线性反馈位的长度，这里是4，如上图的LFSR，之后再分析破解。

img

2.RC4：

  • 初始化一个数组S[]，一般为0-255，这里假设为0-7，S[]:[0,1,2,3,4,5,6,7]。之后初始化一个key顺序数组K[]给定初始密钥顺序，假设为567，重复至8位K[]:[5,6,7,5,6,7,5,6]。

  • 通过KSA算法代码：

1
2
3
4
5
6
7
8
#注释头

j = 0 
for i in range(0,255):
    j = (j + S[i] + K[i])mod 256 
    tmp = S[i]
    S[i] = S[j]
    S[j] = tmp

上述例子得到新的S[]:[5,4,0,7,1,6,3,2]

  • 通过PRGA算法：
1
2
3
4
5
6
7
8
9
10
11
12
13
#注释头

i = 0
j = 0
i = (i + 1)mod 256
j = (j + S[i]) mod 256

tmp = S[i] 
S[i] = S[j] 
S[j] = tmp

t = (S[j] + S[i])mod 256
k = S[t]

上述例子得到K = 6，之后重复8次(n)，即可得到最终密钥K

3.CA：cellular automata

细胞自动机

(1)1D

即一维的：

  • 给定初始状态(一般随机生成)，这里选为0010100(多少bit都行)。

  • 给定状态转换规则，一般给一个十进制数字，然后转换为二进制，这里选为23：

1
2
3
4
#注释头

000 001 010 011 100 101 110 111
 0   0   0   1   0   1   1   1   = 23
  • 依据规则演变至下一个状态(依据当前位和左右邻位)，那么初始状态就可以对应以下七种状态：

000 001 010 101 010 100 000

依据规则转化为 0001000，即为初始状态的之后的第一个状态。依据此规则可演变出多种状态。

  • 再设定规则，从每个状态中取第x位作为密钥，那么n个状态就会对应生成n位的key。

(2)2D

即二维的：原理类似，给定初始状态与规则。

img

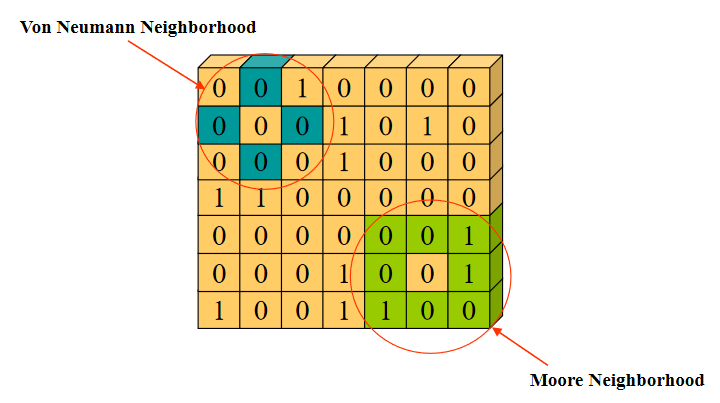
这里的Von Neumann Neighborhood和Moore Neighborhood对应两种不同的邻居选择规则。

▲规则：

img

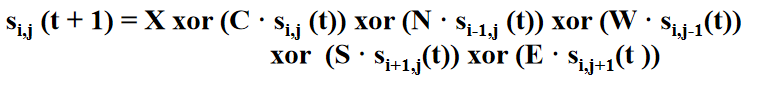
这里的X为自定义的一个初始值0或1，之后的CNSWE分别对应英文certer，north，south，west，east，即中上下左右，加上是一个给定的规则，例如选定：(XCNSWE)为(001110)=14，那么14即为给定的规则。

Si,j(t)即为当前状态分别对应的0或1的值，依据上述等式算出下一状态的值即可。(这里是Von Neumann Neighborhood)

☆针对流密码攻击：插入明文攻击，假设攻击者可以插入1bit的指定明文，再次进行发送，然后也可以截获到密文，那么如下：

img 第一次(只知道密文Ci)

img第二次插入p后(知道密文Ci和p、c)

现在可以通过p^c算出k2，带入第一张图，c2^k2算出p2，再带入第二张图p2^c3算出k3，依次类推可得到全部，除了p1,k1,c1。

第四章 分组密码

1.DES加密(Data Encryption Standard)：

(1)密钥生成：

img

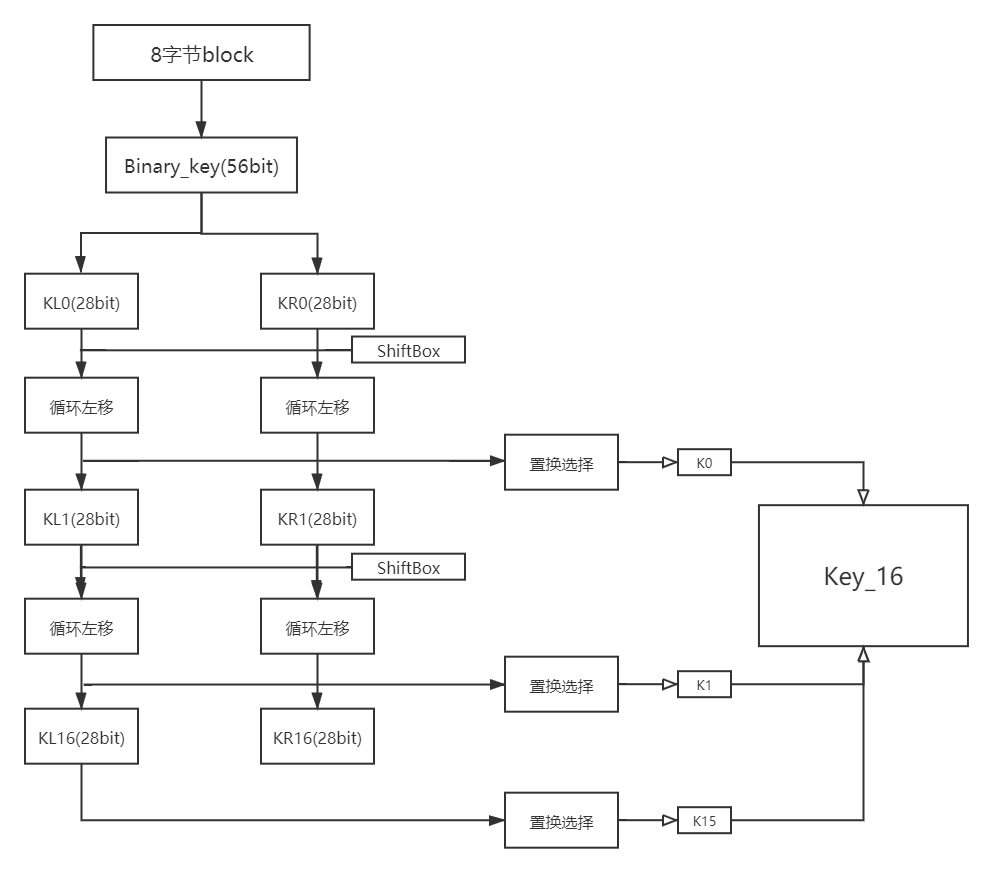
  • 64位密钥，其中8位为奇偶校验位，生成子密钥过程中需要剔除，经过PC-1压缩得到k(56bit)
  • 将k分为KL0和KR0，各28bit
  • KL0和KR0左移x位得到KL0x,KR0x
  • 将KL0x和KR0x合并，通过PC-2置换得到子密钥K0(48bit)
  • 将KL0x和KR0x拷贝一份得到下一轮的KL1和KR1

重复3-5步16轮，共得到k0-k15个子密钥以供加密

(2)加密流程：

img

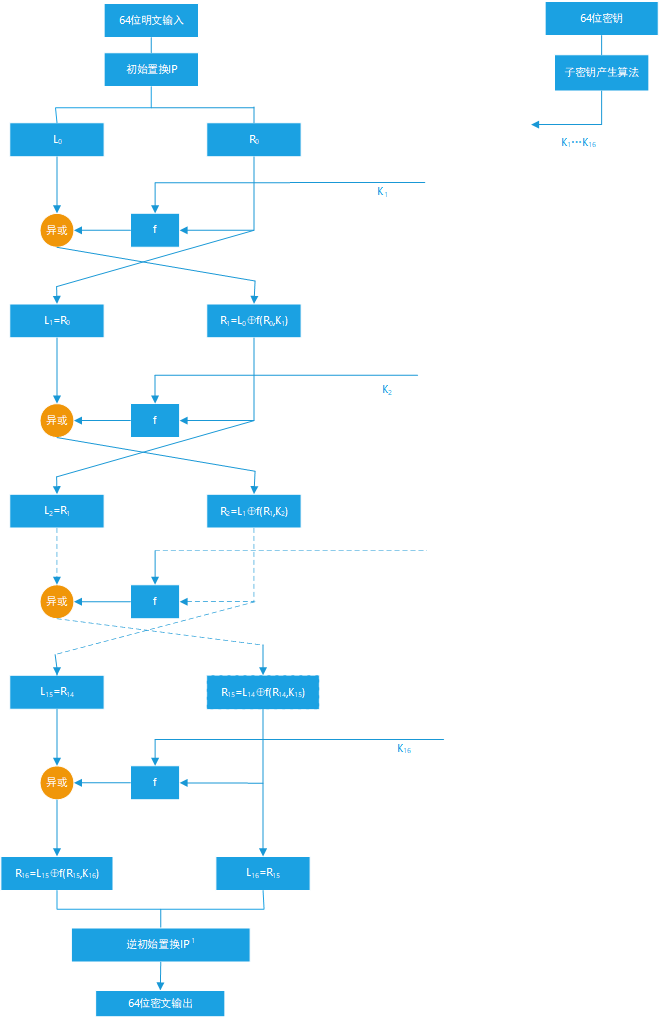
  • 以8个字母为一个单位取明文
  • 将一单位明文通过IT打乱得到Y0
  • 取Y0左边32位为PL0,右边32位为PR0
  • 将PR0复制一份为L1——-用作下一轮的L
  • 将PR0用EBOX扩展置换得到EPR0(48bit)
  • 将EPR0与K0异或得到K_X_P(48bit)
  • 将K_X_P用SBOX压缩得到SPR0(32bit)
  • 将SR0与PBOX进行置换得到PPR0
  • 将PPR0与L0异或得到下一轮的PR1

重复4-9步16轮(其中f轮函数即为EBOX、Key异或、SBOX、PBOX)

▲得到PR15和L15，左右交换后合并在一起后再经过IP逆运算最终置换得到密文

(3)BOX事项：

①EBOX：

虽说是扩展，但直接依据顺序扩展即可。前bit->后bit，后bit->前bit。

img

②SBOX：

8个子BOX，每个子BOX为4×16矩阵，每行0-15以某个固定顺序排列，通过时48bit分为8个块，每个块6bit。首尾bit拼合为row，中间4bit拼合为column，依据(row,column)来在每个子BOX中找到对应的数字后转换为二进制即为4bit输出。

img

之后IP,IP逆,PBOX都是正常的置换BOX。

▲解密流程完全相同，只有密钥使用顺序相反。

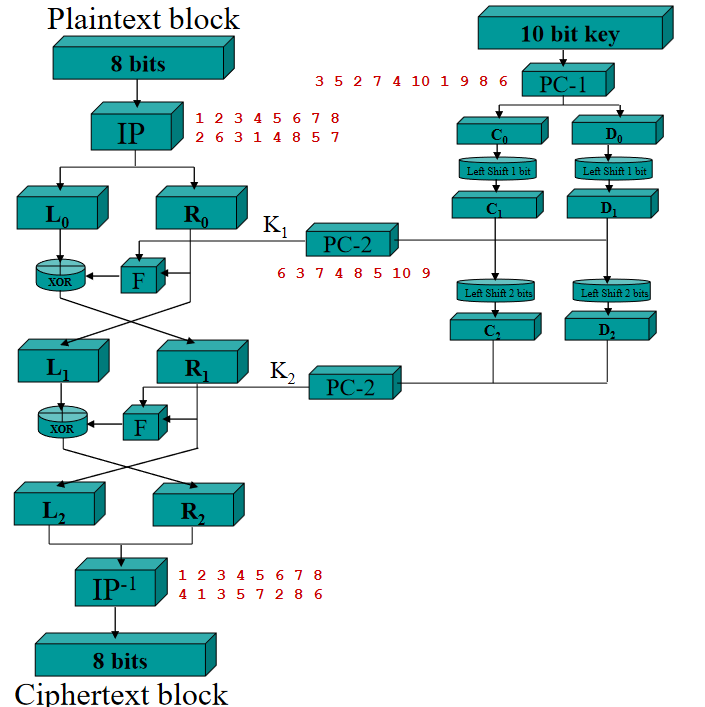
2.SDES加密：

Simple，类似，不过只有两轮，位数也不太一样，分别循环左移1bit和2bit。各种子BOX也会对应修改。

img

3.AES加密(Advanced Encryption Standard):

▲有128bit，192bit和…忘了…以下以128bit为例子

(1)密钥生成：

①前期计算

  • 128bit分为16字节竖向排列：
1
2
3
4
5
6
7
8
#注释头

W0 W1 W2  W3 ..........
-------------------------------------------------------
K0 K4 K8  K12
K1 K5 K9  K13
K2 K6 K10 K14
K3 K7 K11 K15
  • 依据规则计算W[4]至W[43]：

W[i] = W[i-4] xor W[i-1] i不为4的倍数时

W[i] = W[i-4] xor T(W[i-1]) i为4的倍数时

②计算T(W[i-1]):

  • 将W[i-1]中字节元素横向排列，循环左移1个字节。

  • 将循环左移后的四个字节通过SBOX，得到[S0,S1,S2,S3]四个字节列表。(这个SBOX为16×16矩阵，需要将每个字节的前4bit作为row，后4bit作为column，(row,column)来在SBOX中寻找对应字节替换)

img

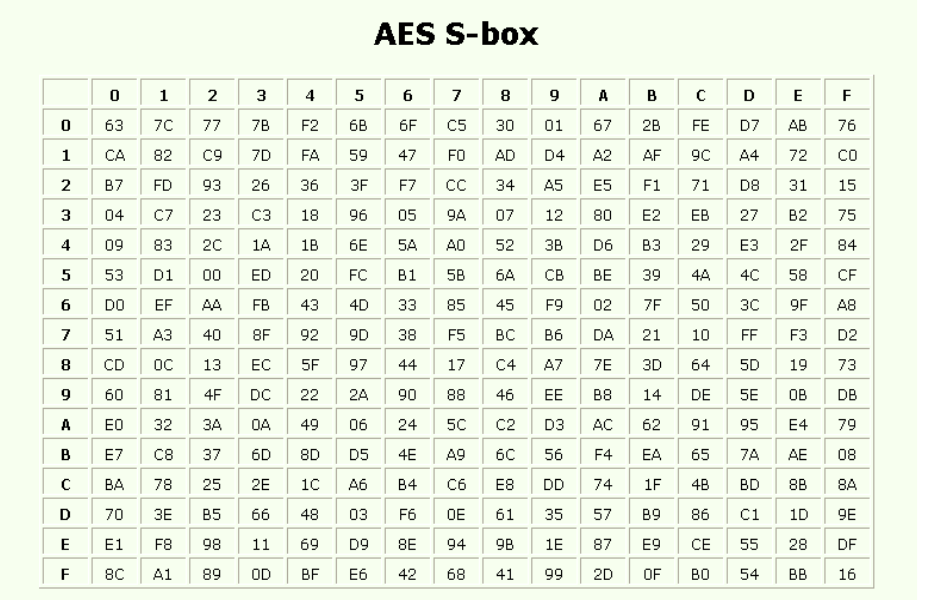
  • 计算常量：r[i] = 2^((i-4)/4)

  • 最终T(W[i-1]) = [S0 xor r(i),S1,S2,S3]

即可求得W[0]-W[43]共计44个W[i]密钥。

(2)加密流程：

img

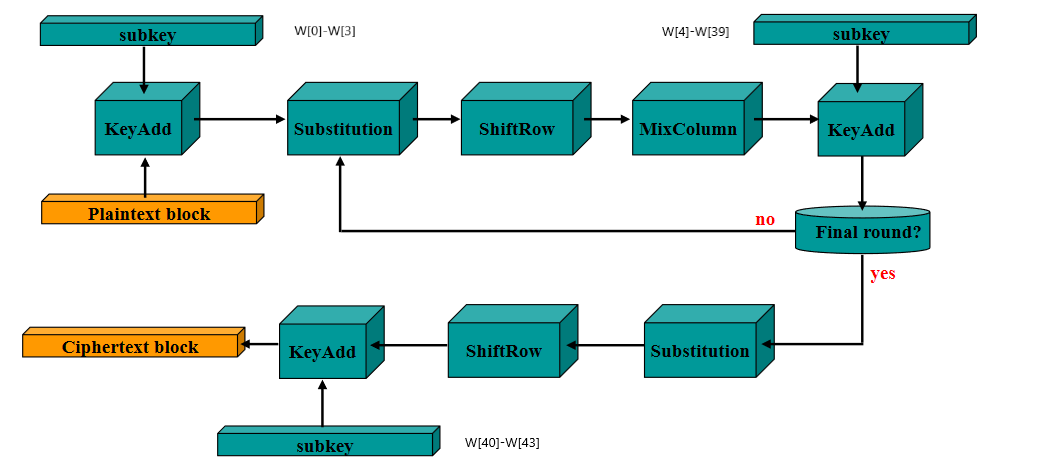
128bit输入，循环9轮，第10轮中没有MixColumn。

(3)BOX注意：

  • KeyAdd：正常的128bit密钥和128bit明文块异或。

  • Substitution：即SBOX，为