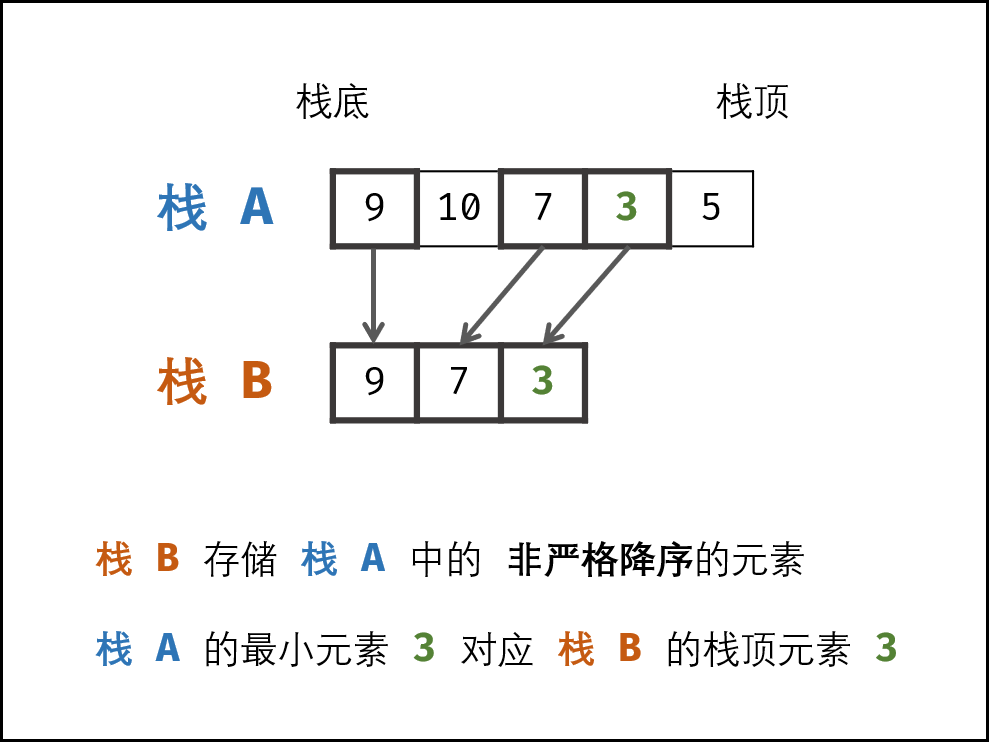
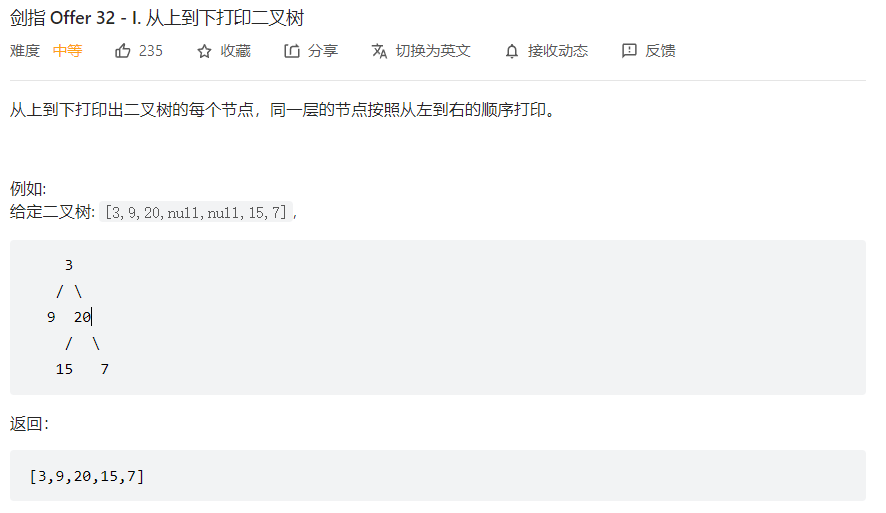
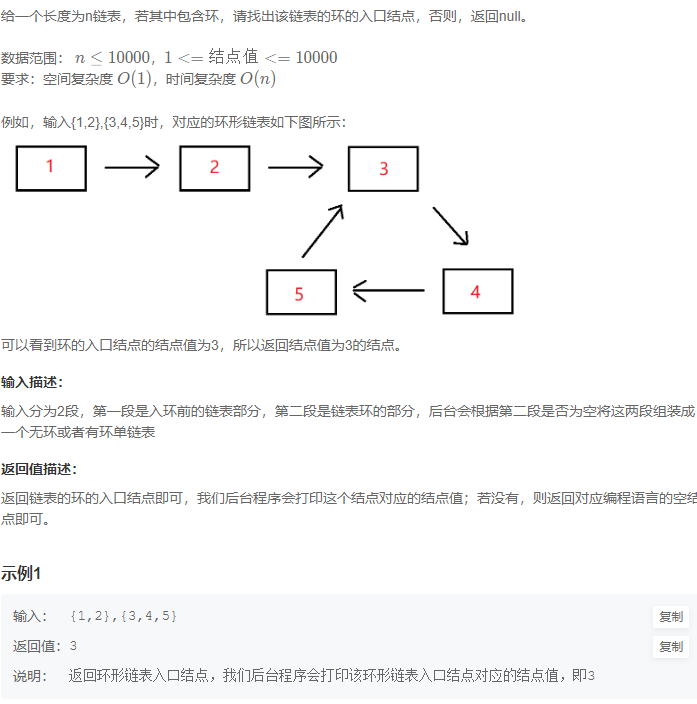
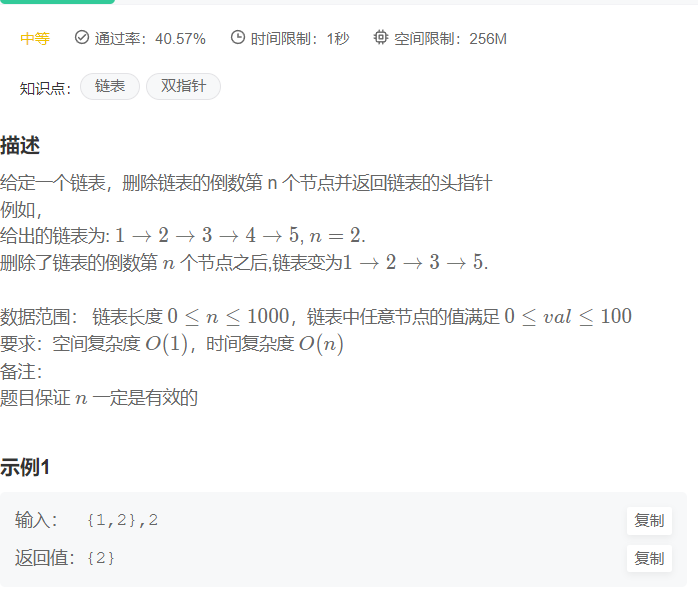
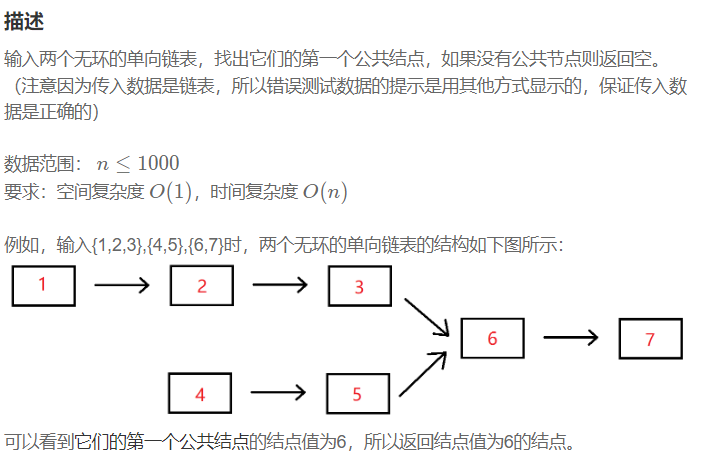
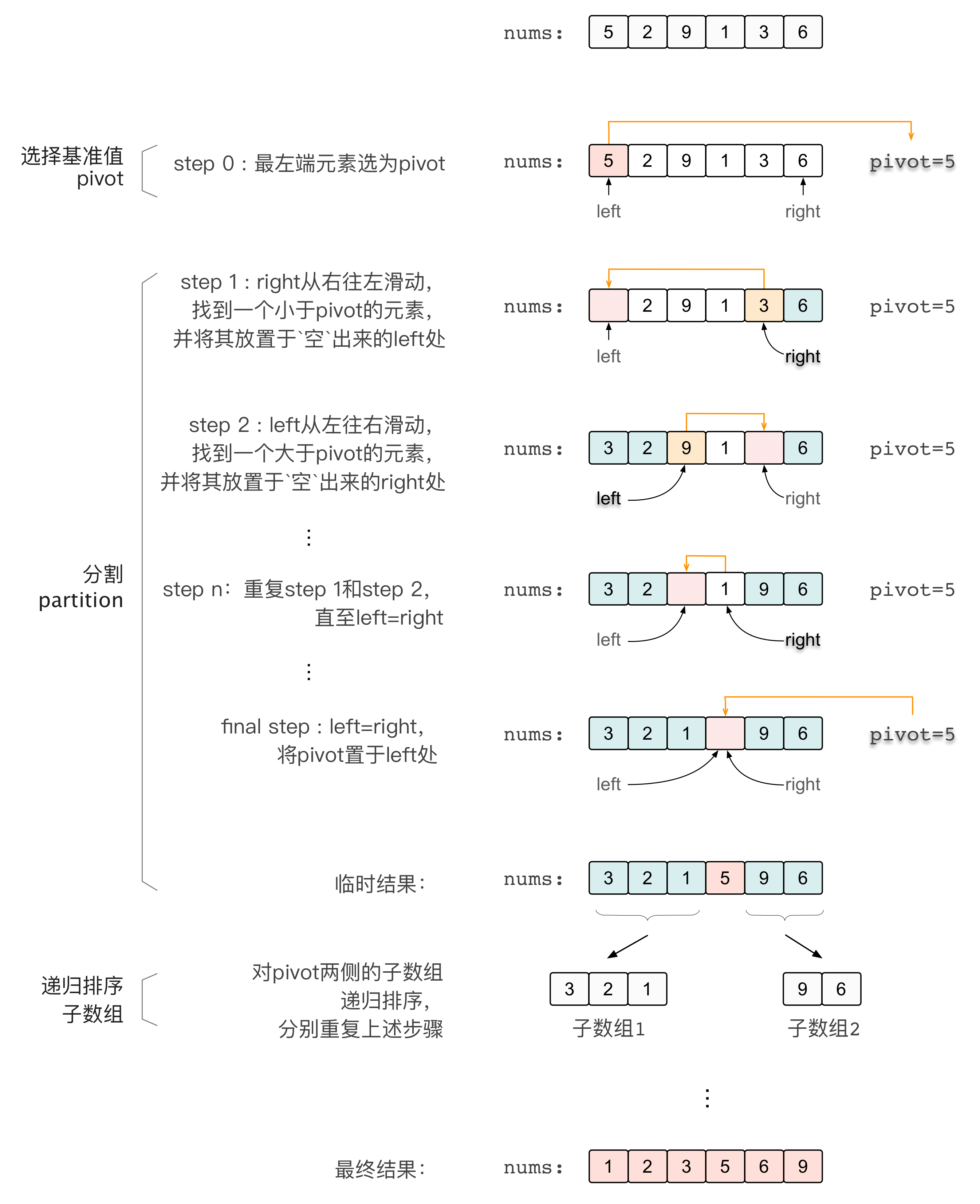
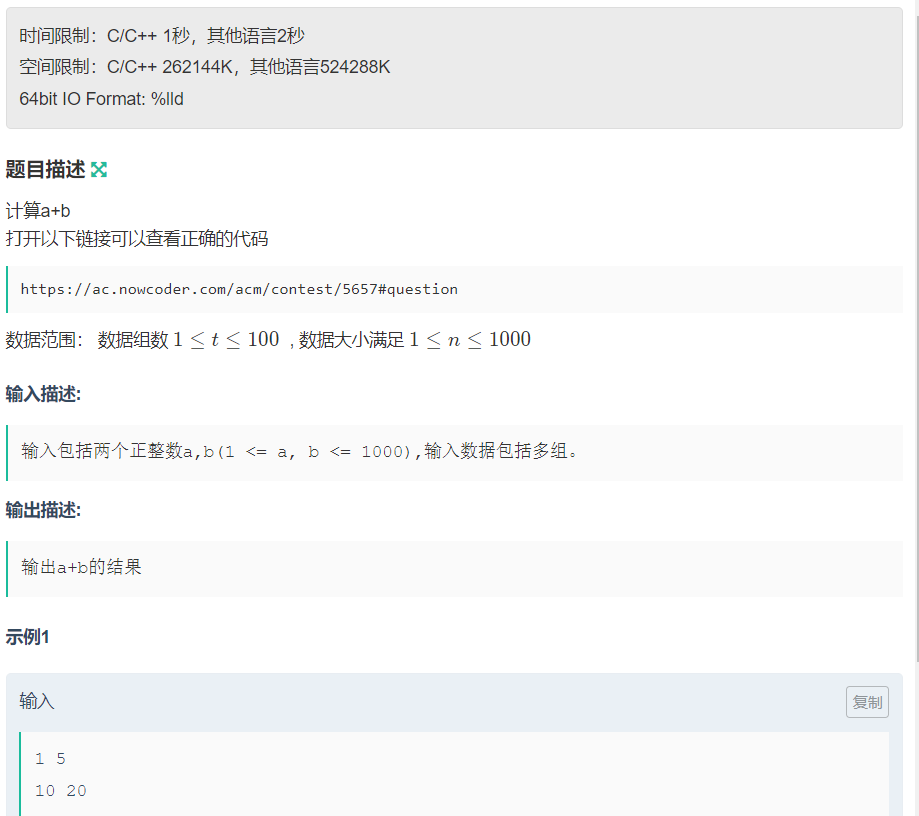
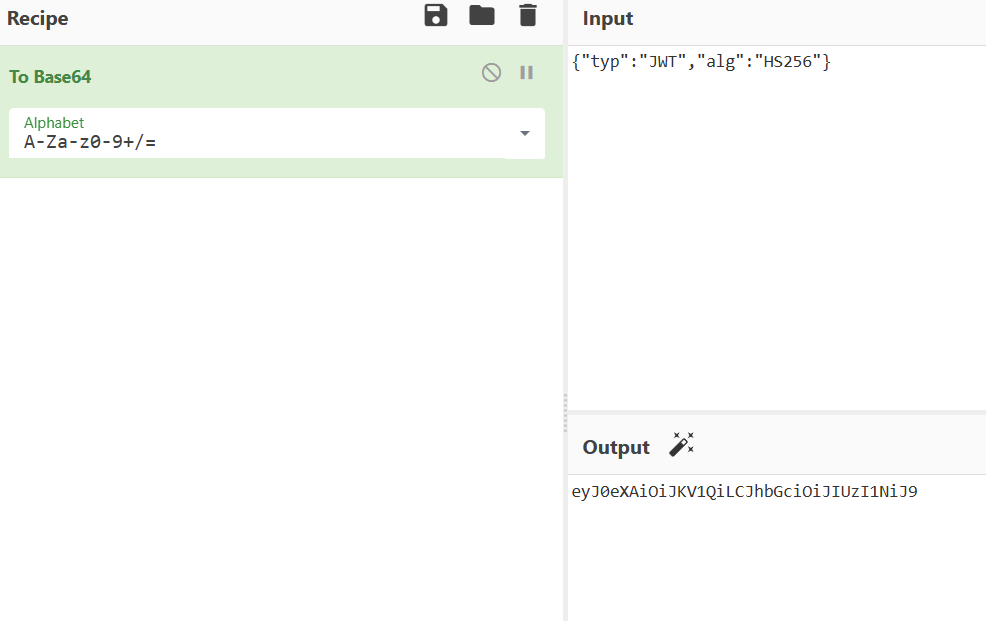
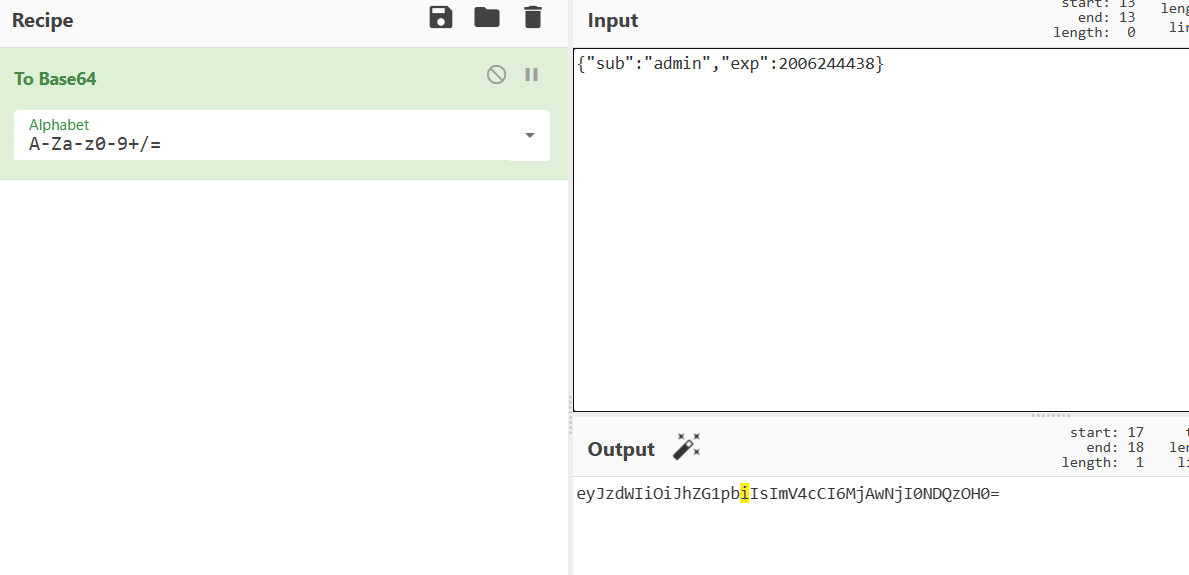
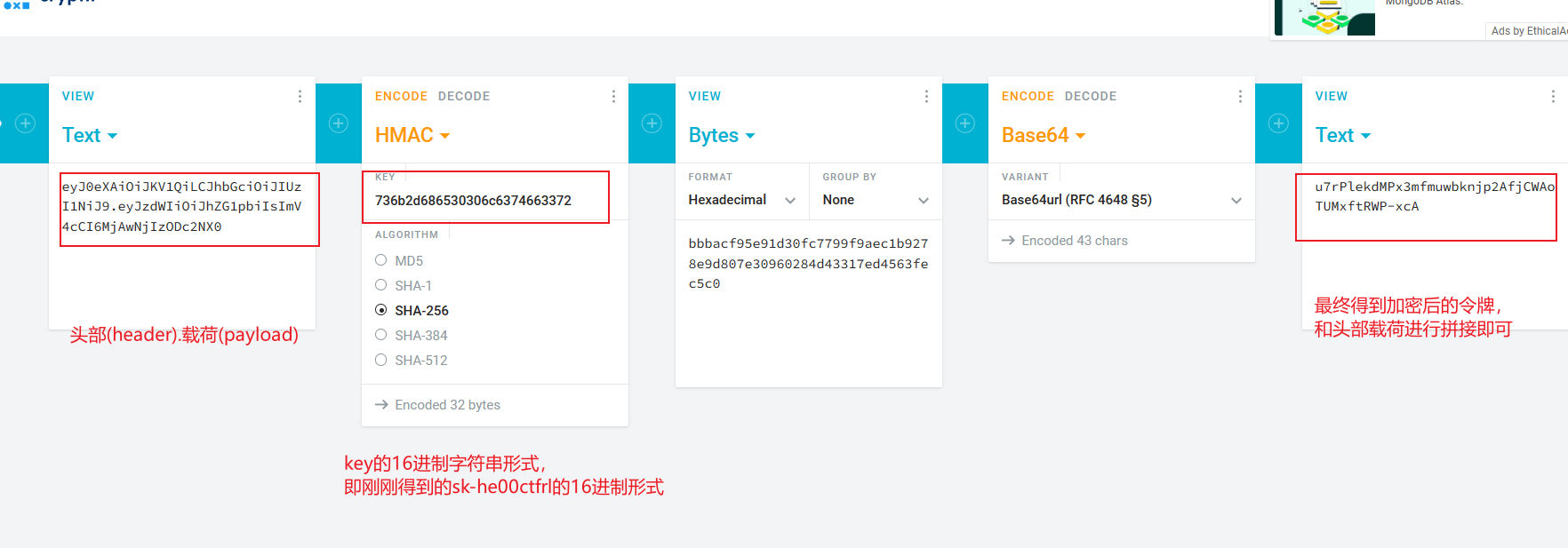
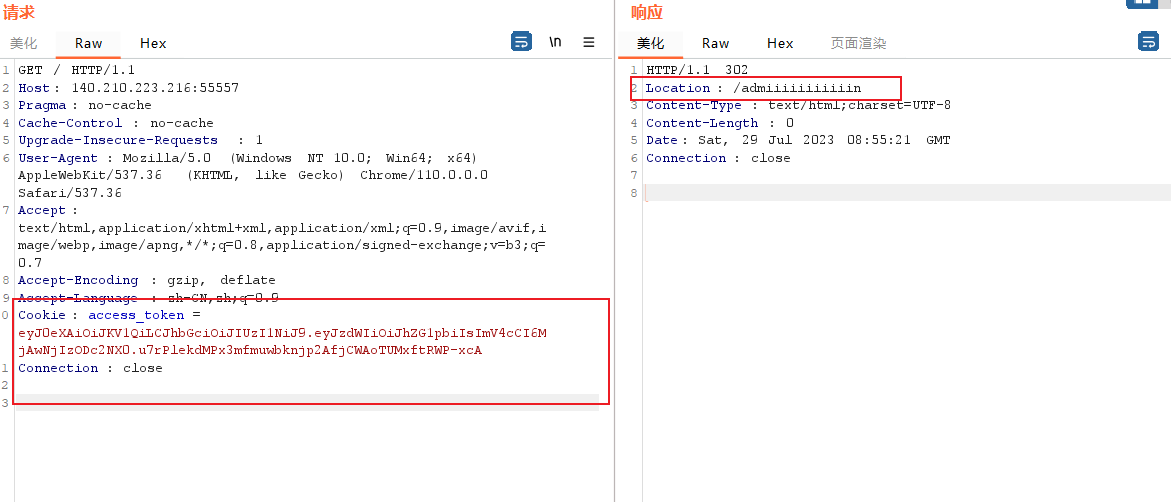
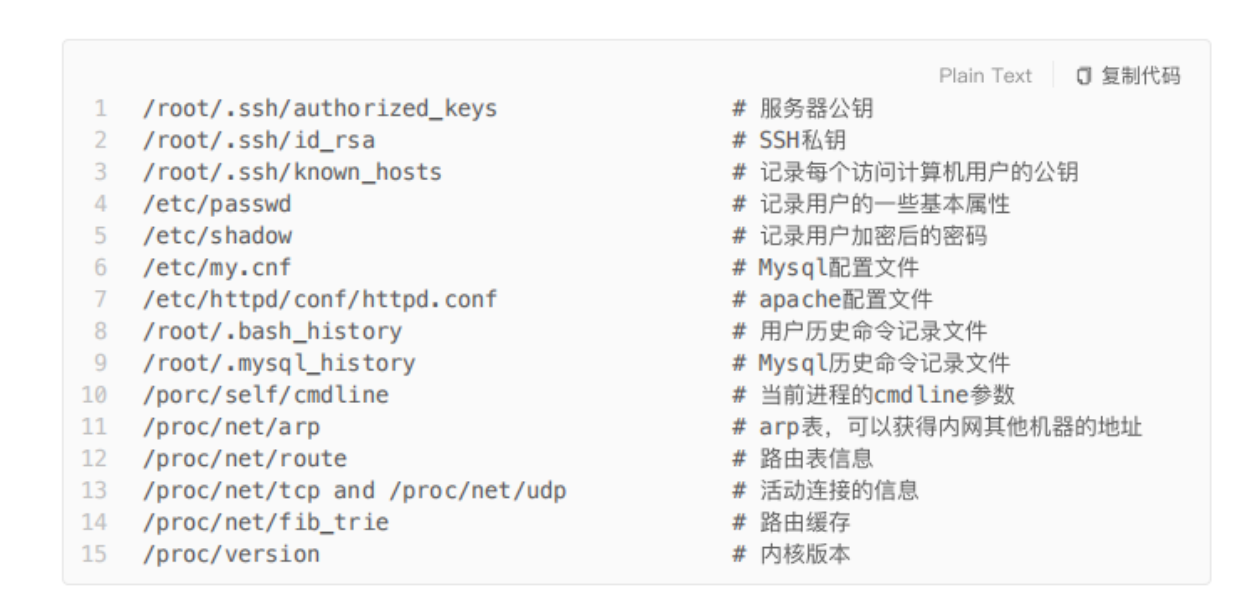
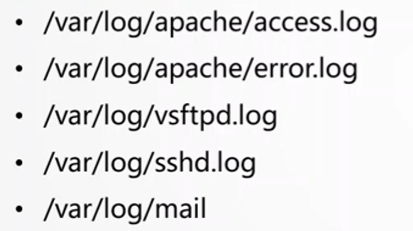
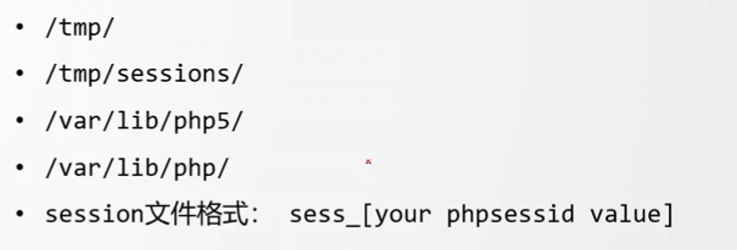
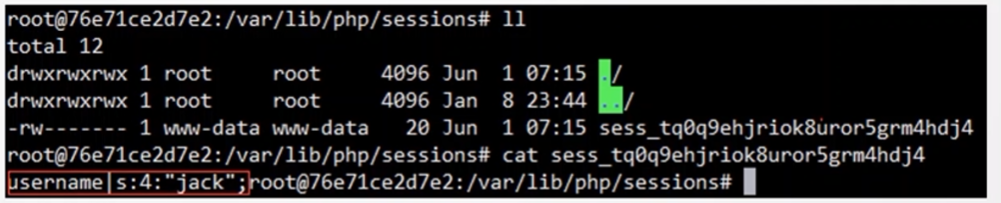
前言
南京大学《软件分析》课程笔记
南京大学《软件分析》课程01(Introduction)_哔哩哔哩_bilibili
一、Intermediate Representation

1.中间语言编译
(1)过程
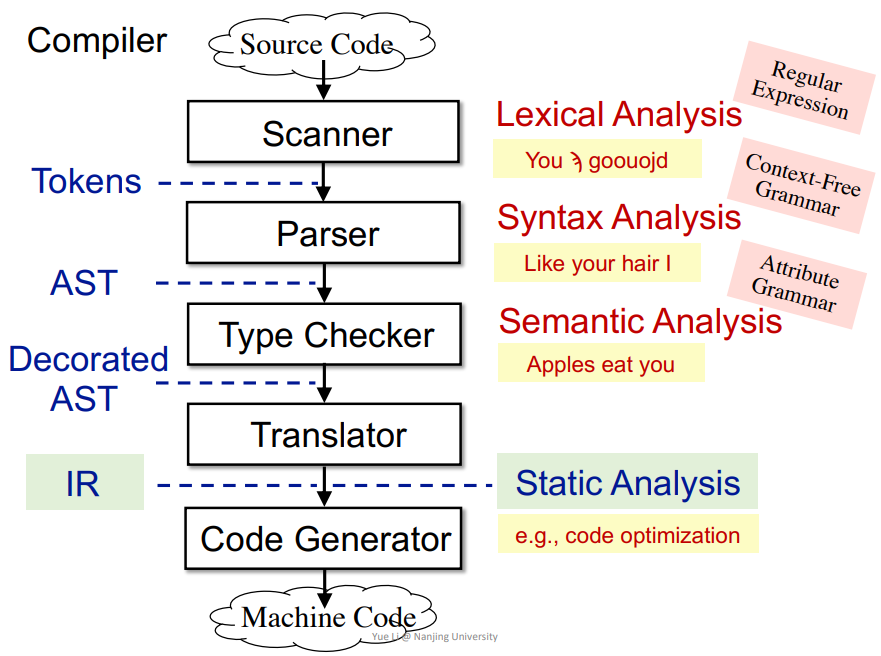
- 词法分析(
Lexical Analysis):从源代码到Tokens,检测单词是否正确 - 语法分析(
Syntax Analysis):从Tokens到AST,检测语法是否正确 - 语义分析(
Semantic Analysis):从AST到Decorated AST,检测语义或者说上下文,语境是否正确,比较复杂,一般在编程语言中不会涉及到,主要是自然语言才有的。 - 转换(
Translator):从AST到IR,即转换为三地址码,方便识别,最后生成机器码
(2)AST和IR
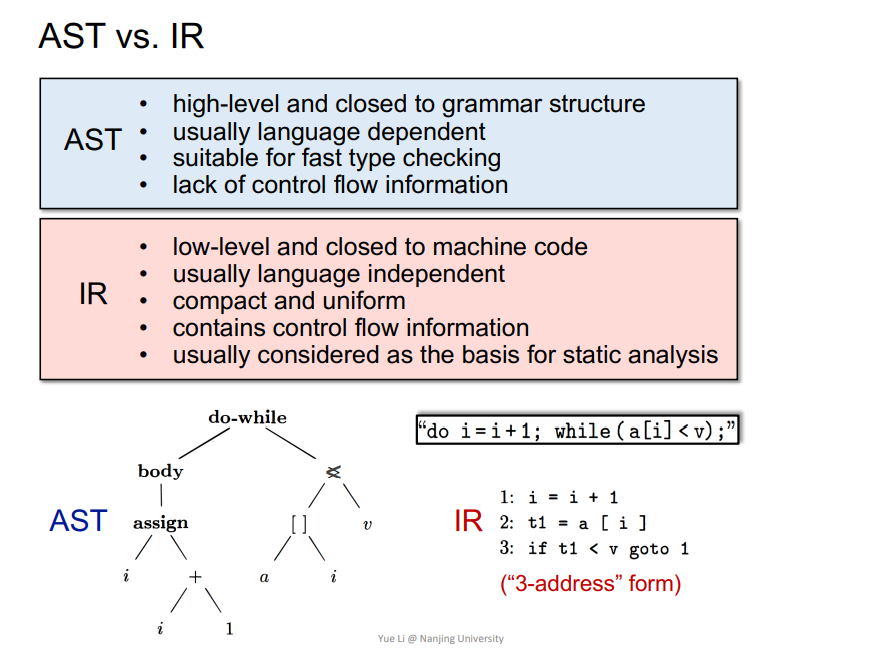
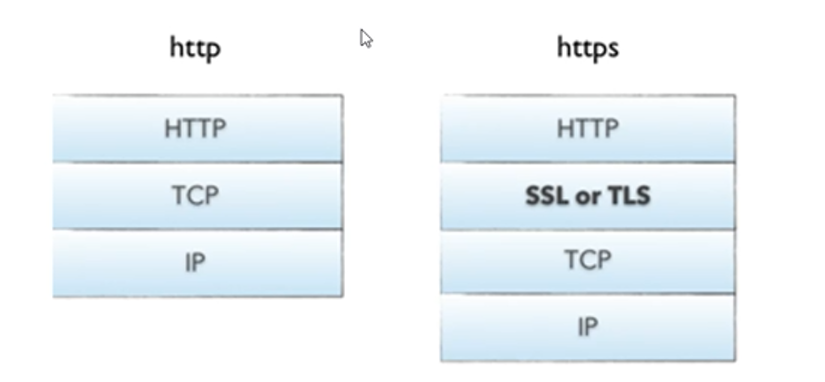
IR更利用静态分析,因为能够展现控制流程,语言无关性,更贴近于机器码。
2.Soot常见分析
从JAVA代码到三地址码
For循环例子
1 | public class ForLoop3AC{ |
转换为
1 | public static void main(java.lang.String[]){ |
do-while以及数组例子
1 | public class DoWhileLoop3AC{ |
转换为
1 | public static void main(java.lang.String[]){ |
函数调用例子
1 | public class MethodCall3AC{ |
转换为
1 | java.lang.String foo(java.lang.String, java.lang.String){ |
这里有个关于函数调用的知识点

不同invoke在三地址码中代表调用不同的函数,是在JVM虚拟机中的一种表示。
- 在
<method signature>中的method signture通常结构为class name: return type method name(parameter1 type)
静态变量和类
1 | public class Class3AC{ |
转换为
1 | public class nju.sa.examples.Class3AC extends java.lang.Object{ |
3.SSA(Static Single Assignment)
和三地址码3AC类似的一种表达方式,有优点也有缺点,但是大多用的是3AC,对于SSA区别如下
- 每个定义的变量都有自己的不同名字
- 每个变量都有自己的定义
比如

如果有多的相同变量,则会有一个函数来判断,如下
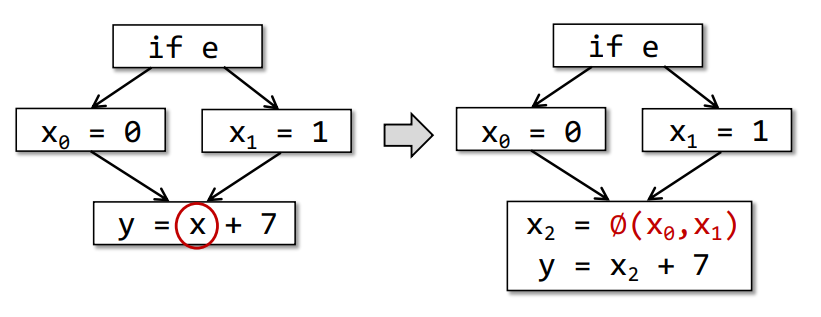
即X2 = ∅(X0,X1) 会用来判断值到底是哪个
4.基础块(Basic Block)
定义:
- 只有一个入口指令,入口指令为第一个指令
- 只有一个出口指令,出口指令为最后一个指令
- 一个跳转目的点应该是一个
BB的入口指令
方法:
如下为例子

首先确定程序中入口
即**(1)**为入口

然后确定跳转指令的目的地址,标记为
leader,依据指令**(4)、(10)和(11)即可确定这里即为(3)、(7)和(12)**
跳转指令后面的指令为一个
leader,依据指令**(4)、(10)和(11)即可确定这里即为(5)、(11)、(12)**
依据
leader来划分BB,即一个BB应该是由一个leader到下一个leader之间的所有指令构成,不包括下一个leaderleaders: (1), (3), (5), (7), (11), (12)划分
BB:BB1:**(1)~(2)**BB2:**(3)~(5)**BB3:**(5)~(6)**BB4:**(7)~(10)**BB5:**(11)**BB6:**(12)**
得到最终
BB结构
5.CFG(Control Flow Graph)
定义:
- 每个节点
node为一个BB - 两个节点
node之间只能有一条边
方法:
首先跳转指令的跳转目的地址都修改为对应的
BB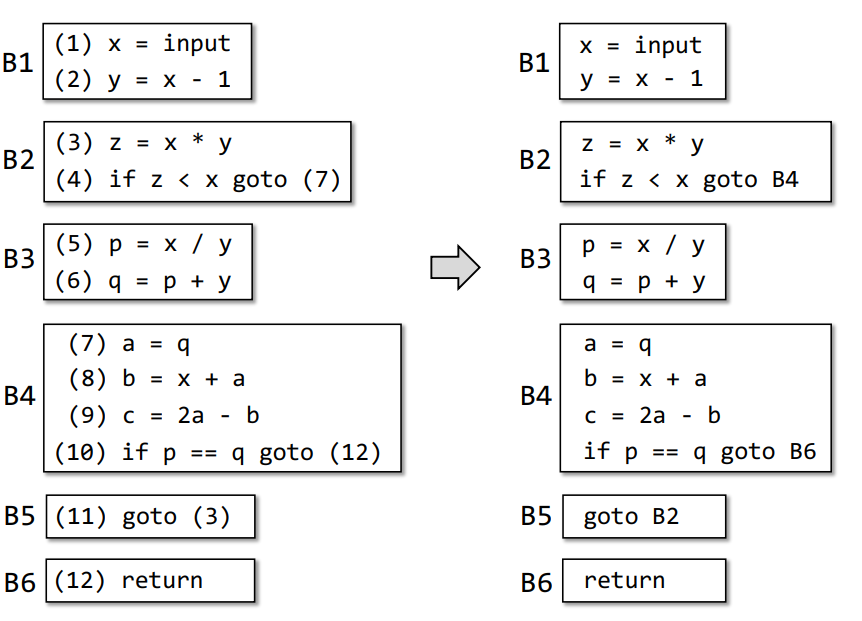
然后依据跳转指令,将对应跳转进行连边,即得到
B2->B4、B4->B6、B5->B2三条边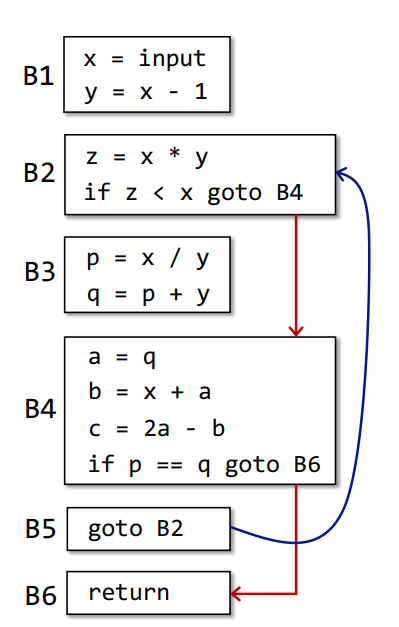
从程序入口到程序出口间所有的
BB,由上至下两两添加一条边,除了包含无条件跳转的BB,那么得到B1->B2、B2->B3、B3->B4、B4->B5四条边,由于B5出口指令为无条件跳转,所以B5->B6没有边,得到如下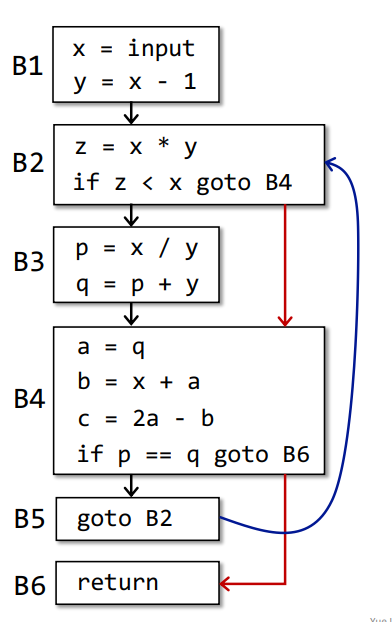
依据边的方向,得到各个
BB之间的前驱后继的关系加入
Entry和Exit,得到如下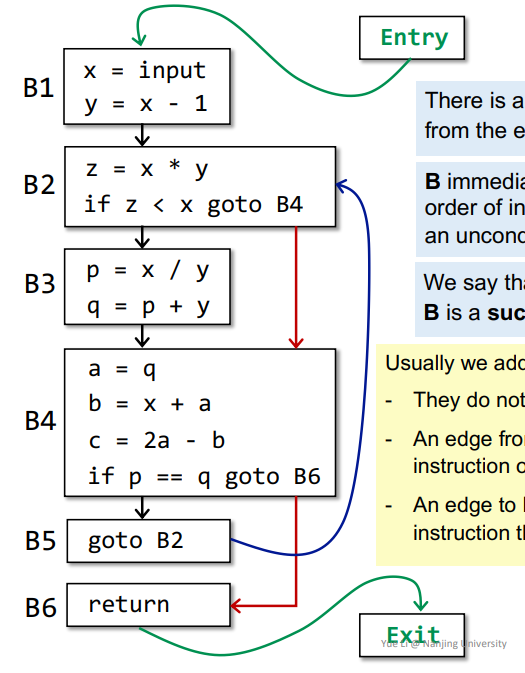
二、Data Flow Analysis I

即数据(DATA)在CFG(Control Flow Graph)中Flow的过程分析
1.基本概念
常见符号
抽象符号
⊥:未定义+、-:常见正负表示0:即零
IN[S]和OUT[S]
一个IR语句的输入数据集合以及输出数据集合,如下所示
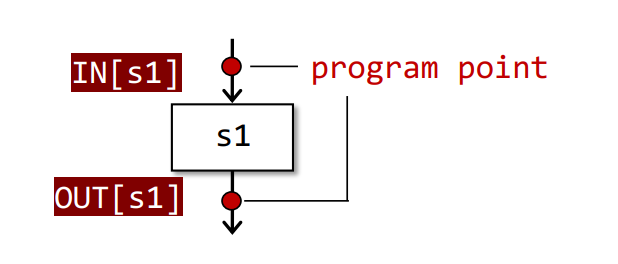
然后也区分几种状况,如下所示
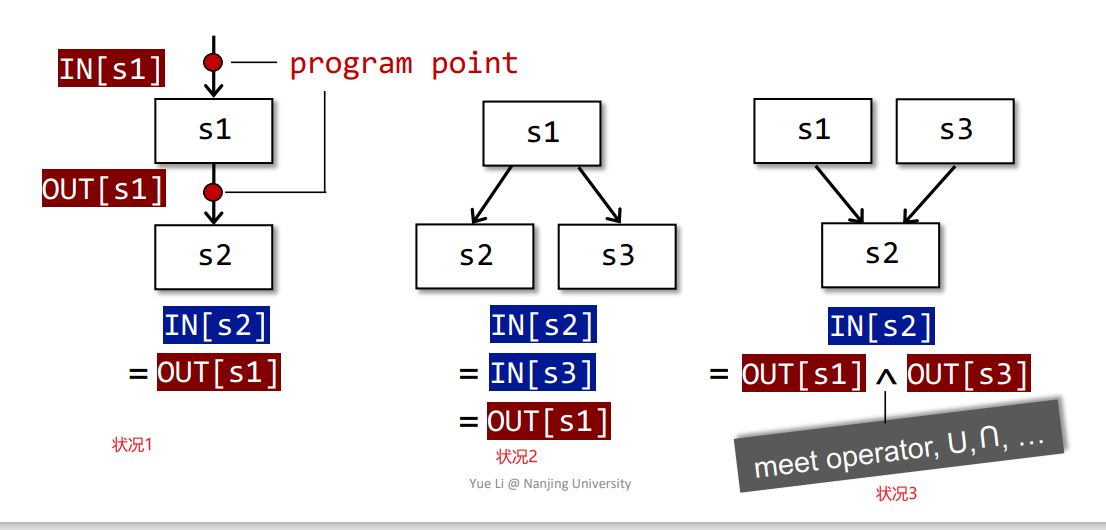
状况1:
IN[S2] = OUT[S1],常见流程状况2:
IN[S2]、IN[S3] = OUT[S1],分支流程状况3:
IN[S2] = OUT[S1] ^ OUT[S3],交汇流程其中的合并操作称为
meet操作,常见有取交集、并集之类的,需要定义
分析方向
Forward Analysis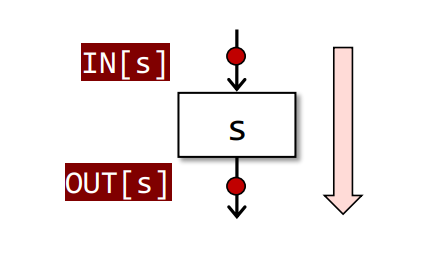
相关公式
$$
OUT[s] = f_s(IN[s])
$$Backward Analysis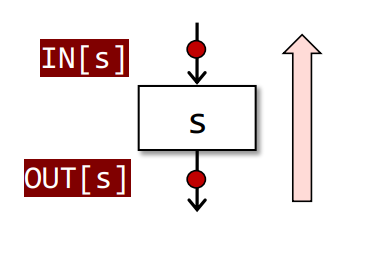
相关公式
$$
IN[s] = f_s(OUT[s])
$$
2.BB之间的分析
在一个基本块
BB中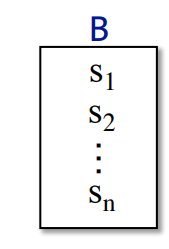
IN[s]以及OUT[s]可以用一个循环表示
$$
IN[s_{i+1}] = OUT[s_i], for\ all\ i = 1,2, …, n-1\
OUT[s_i] = f_s(IN[s_{i-1}])
$$同样的多个基本块
BB中- 即
B1 -> B2 -> B3这样的
$$
IN[B] = IN[s_1], OUT[B] = OUT[s_n]\
OUT[B] = f_B(IN[B]), f_B = f_{sn} \ ⚬ \ …\ ⚬\ f_{s2}\ ⚬\ f_{s1}
$$当然还有其它的,交汇
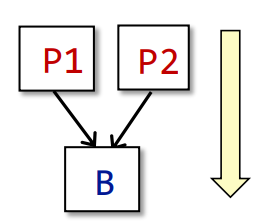
1
IN[B] = ^p OUT[p]
其中
^p代表取所有的p做meet操作还有分支,分支的
OUT[B]都等于下一个的IN[B.]
- 即
3.Reaching Definition
即一个变量v从定义点p,到某一点q这条路径中,v没有再被重新定义,那么这条路径可以被当作Reaching Definition,如果再被重新定义了,则不能,如下
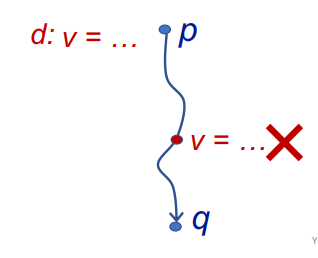
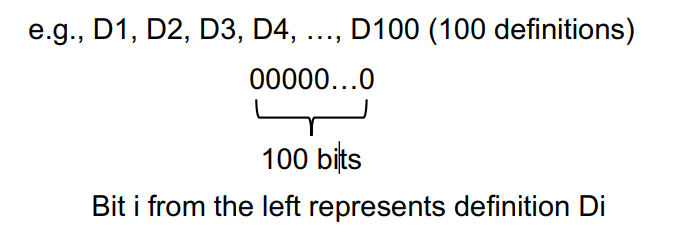
Data Flow Facts
将所有定义变量的语句标记为一个bit向量
Control Flow
用来求IN[B],例子如下
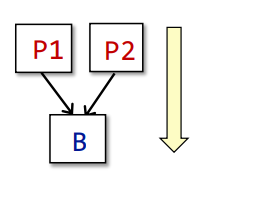
1 | IN[B] = Up predecessor of B OUT[p] |
其中Up代表取B的前驱,即所有的p做union操作,即并集
Transfer Function
即数据流分析中的转换函数的相关定义,forward下知道IN[B]用来求OUT[B]
$$
OUT[B] = gen_B\ U\ (IN[B] - kill_B)
$$
genB:表示当前基本块中定义的所有变量的合集killB:表示当前基本块中定义的所有变量,并且这些变量在其他基本块中也被定义了的合集
例子如下
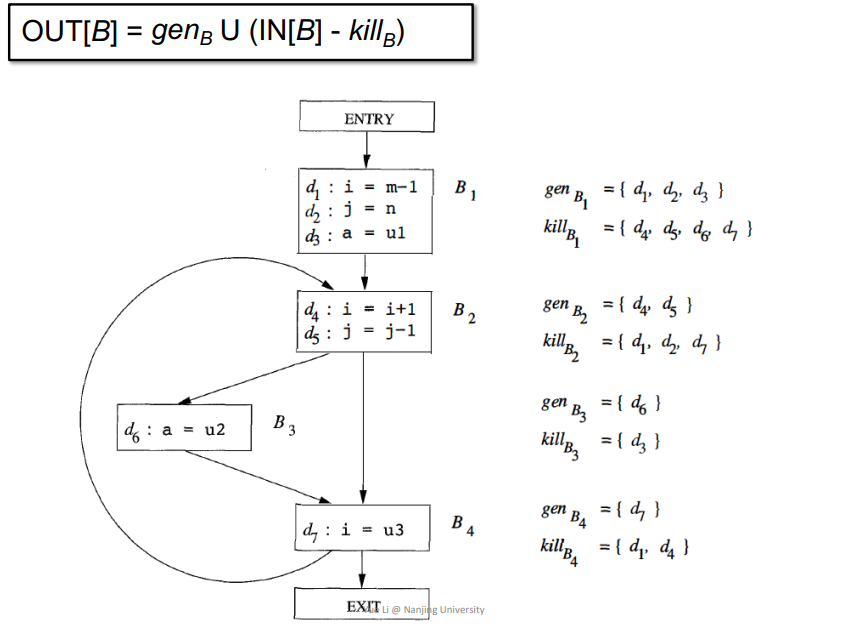
Algorithm

其中对于每个BB的赋值,在may analysis中大多为空,而在must analysis中大多不为空,所以并没有把OUT[entry] = ∅; 加进来
例子
如下所示,初始化之后即可迭代
第一次迭代
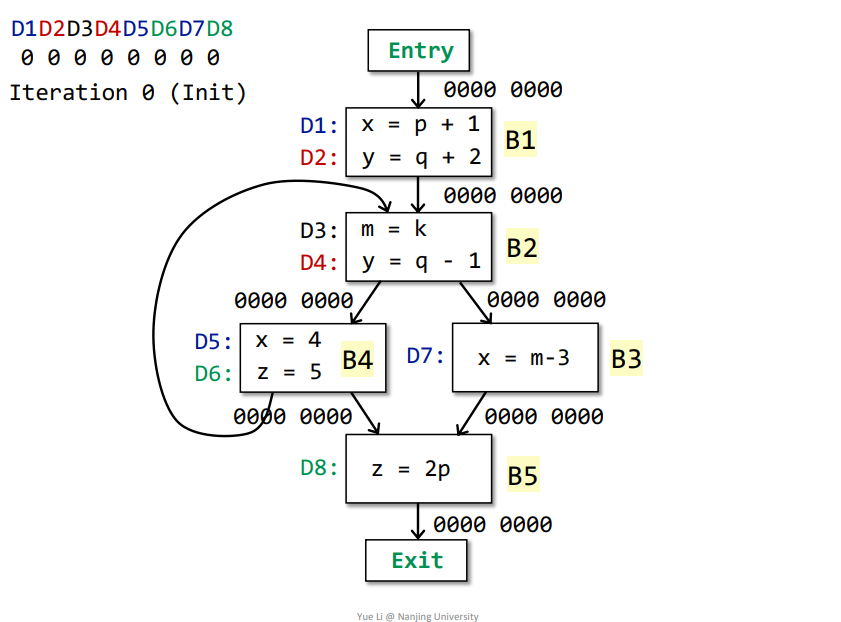
Entry->B1:OUT[Entry] = 0000 0000IN[B1] = Up OUT[p] = OUT[Entry] = 0000 0000genB1 = D1 + D2 = 1100 0000killB1 = D5 + D7 + D4 = 0001 1010IN[B1] - killB1 = 0000 0000 - 0001 1010 = 0000 0000都是0,减去之后还是0
OUT[B1] = genB1 U (IN[B1] - killB1) = 1100 0000 + 0000 0000 = 1100 0000
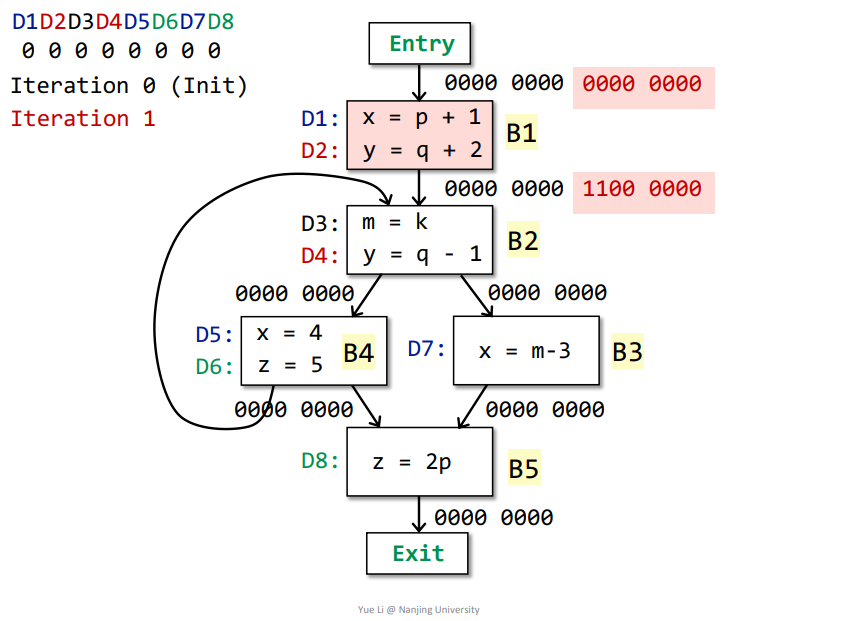
B1->B2:OUT[B1] = genB1 U (IN[B1] - killB1) = 1100 0000 + 0000 0000 = 1100 0000IN[B2] = Up OUT[p] = OUT[B1] + OUT[B4] = 1100 0000genB2 = D3 + D4 = 0011 0000killB2 = D2 = 0100 0000IN[B2] - killB2 = 1100 0000 - 0100 0000 = 1000 0000OUT[B2] = genB2 U (IN[B2] - killB2) = 0011 0000 + 1000 0000 = 1011 0000
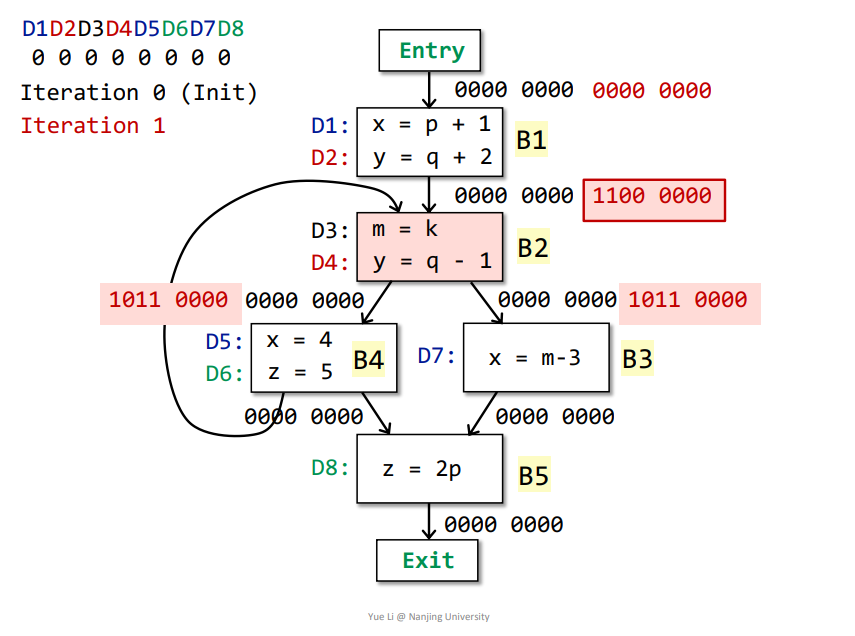
B2->B3:OUT[B2] = genB2 U (IN[B2] - killB2) = 0011 0000 + 1000 0000 = 1011 0000IN[B3] = Up OUT[p] = OUT[B2] = 1011 0000genB3 = D7 = 0000 0010killB3 = D1 + D5 = 1000 1000IN[B3] - killB3 = 1011 0000 - 1000 1000 = 0011 0000OUT[B3] = genB3 U (IN[B3] - killB3) = 0000 0010 + 0011 0000 = 0011 0010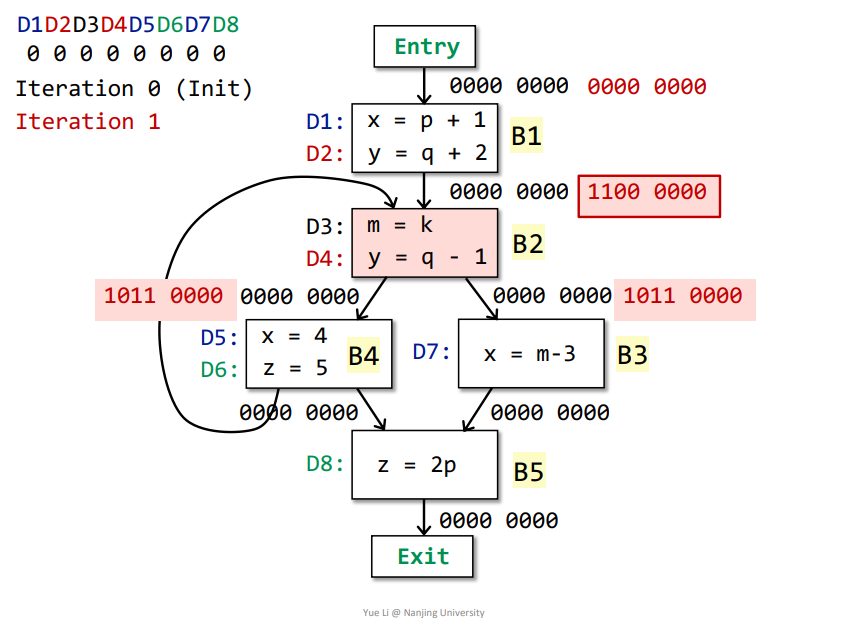
B2->B4:OUT[B2] = genB2 U (IN[B2] - killB2) = 0011 0000 + 1000 0000 = 1011 0000IN[B4] = Up OUT[p] = OUT[B2] = 1011 0000genB4 = D5 + D6 = 0000 1100killB4 = D1 + D7 + D8 = 1000 0011IN[B4] - killB4 = 1011 0000 - 1000 0011 = 0011 0000OUT[B4] = genB4 U (IN[B4] - killB4) = 0000 1100 + 0011 0000 = 0011 1100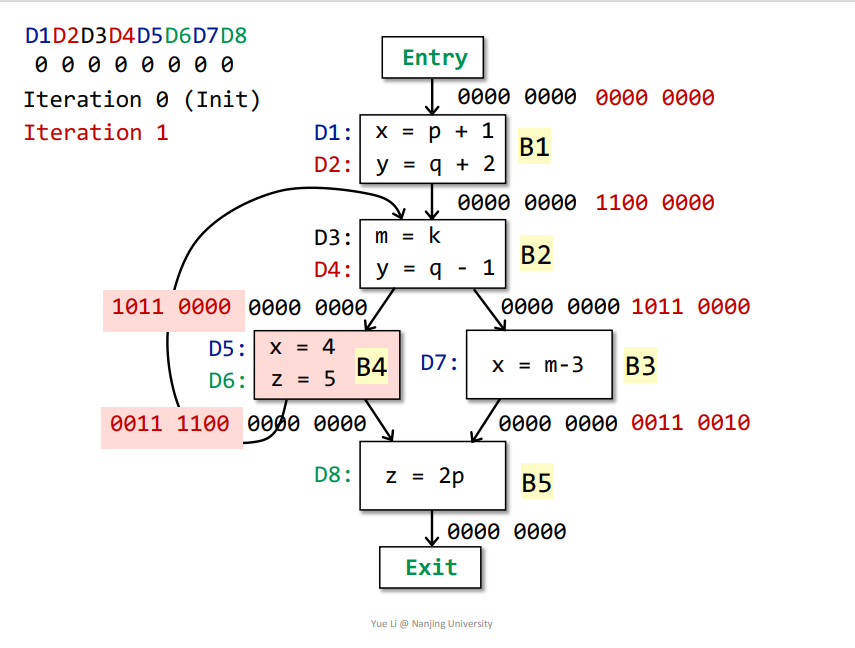
B4、B3->B5OUT[B3] = genB3 U (IN[B3] - killB3) = 0000 0010 + 0011 0000 = 0011 0010OUT[B4] = genB4 U (IN[B4] - killB4) = 0000 1100 + 0011 0000 = 0011 1100IN[B5] = Up OUT[p] = OUT[B3] + OUT[B4] = 0011 0010 + 0011 1100 = 0011 1110genB5 = D8 = 0000 0001killB5 = D6 = 0000 0100IN[B5] - killB5 = 0011 1110 - 0000 0100 = 0011 1010OUT[B5] = genB5 U (IN[B5] - killB5) = 0000 0001 + 0011 1010 = 0011 1011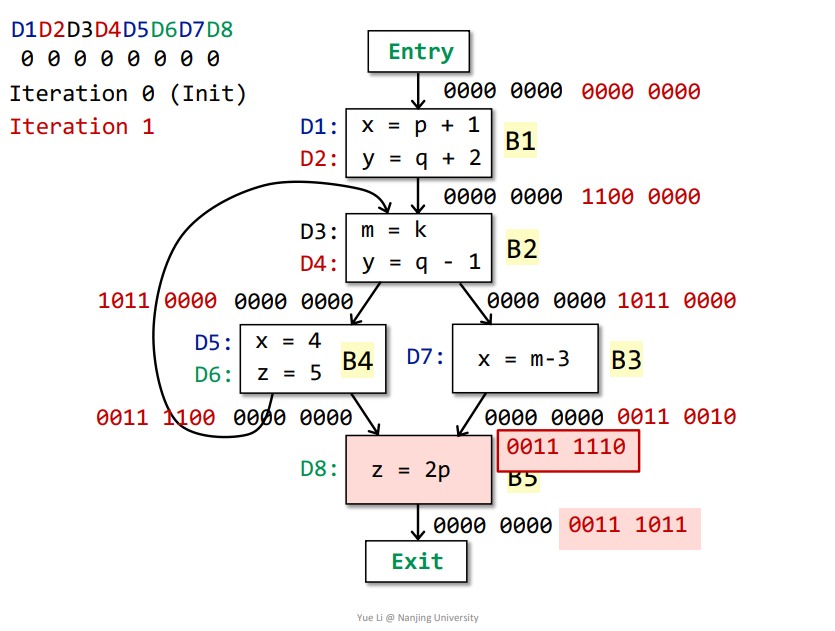
那么由于第一次迭代之后,B1、B2、B3、B4、B5的OUT都发生改变了,所以继续迭代,所有基本块的OUT被本次迭代结果替换
第二次迭代
完成如下
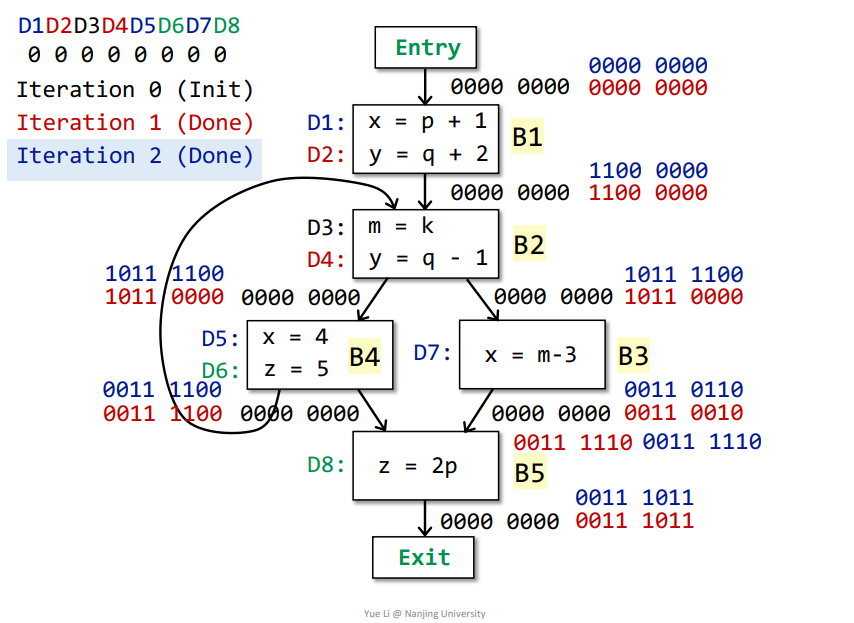
那么基本块B2、B3的OUT发生了改变,接着迭代
第三次迭代
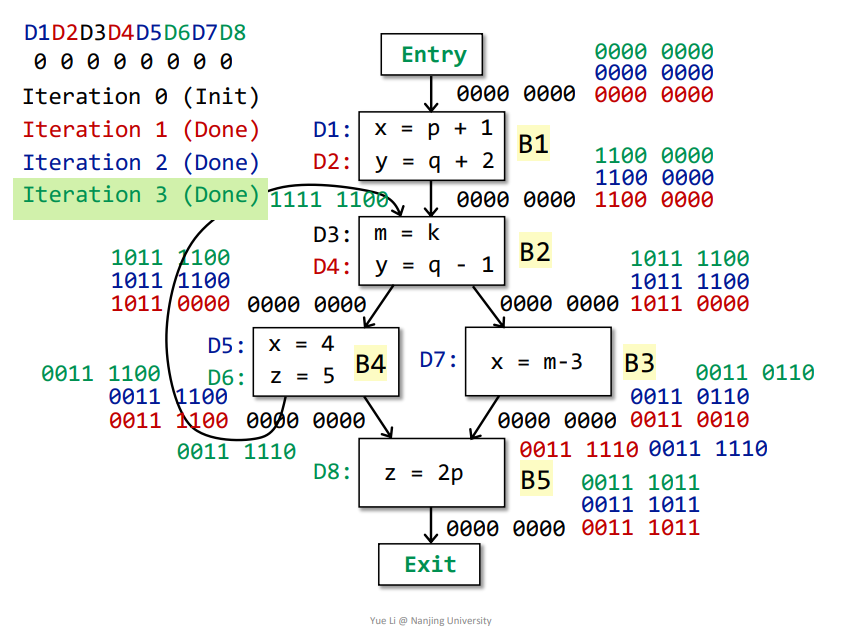
迭代之后,所有基本块的OUT都没有发生改变,那么即可得到最终结果。
最终含义
依据最终结果,即所有基本块的OUT[Bn]可得,比如对于OUT[B1]而言,对应结果为1100 0000,代表D1、D2可以Reach到B1结束的地方,也就是说D1、D2所定义的变量从被定义到B1结束的地方都不会被改变。
三、Data Flow Analysis - Applications II
1.Live Variables Analysis
即存在一个变量v在点p被定义,然后程序中还存在一个变量v被使用的地方use(v),满足从p到use(v)这条路径上,v没有被重新定义,那么可以称为变量v在点p到use(v)这条路径上是存活的,如下

- 应用
比如寄存器满的状态,这时候在p点发现变量v是dead的,并且该变量在寄存器中,那么新的变量最好就是替换掉dead变量v。
Data Flow Facts
将所有变量的标记为一个bit向量,和之前类似,1表alive

Control Flow
用来求OUT[B]的,例子如下
1 | OUT[B] = Us successor of B IN[S] |
其中Us代表取B的后继,即所有的s做union操作,即并集
Transfer Function
由于是backward,所以即知道OUB[B]来求IN[B]
$$
IN[B] = use_B\ U\ (OUT[B]\ -\ def_B)
$$
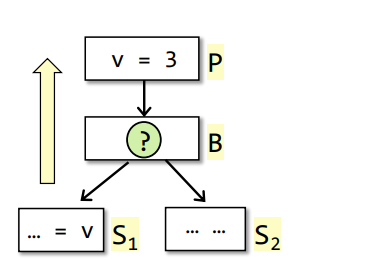
useB:在基本块BB中在重定义之前被使用的变量的合集比如某个基本块
v = 2; k = v,由于v是在被重定义之后被使用的,所以变量v不被归入到useB中defB:在基本块BB中被重定义或首次定义的变量的合集
Algorithm

同样进行简单初始化即可开始迭代
例子
如下所示,初始化之后即可迭代
第一次迭代
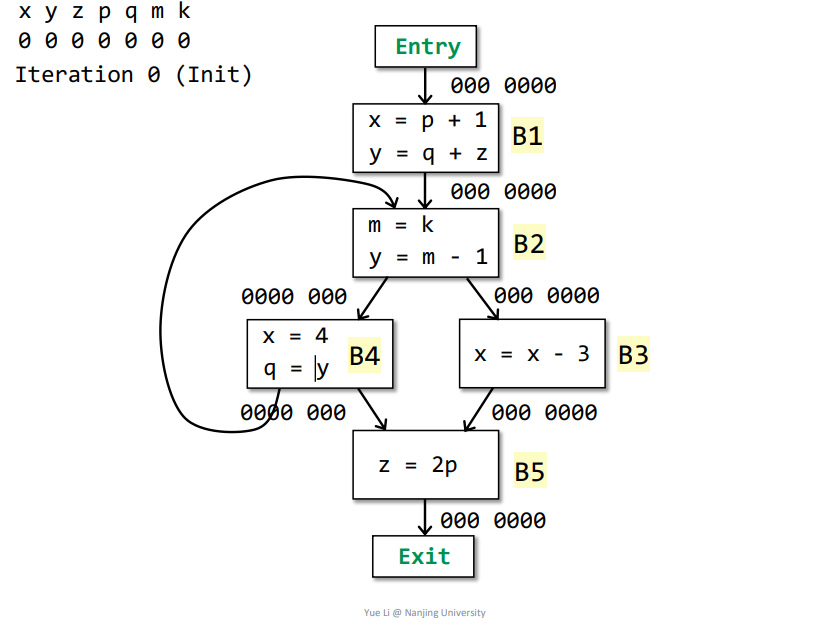
Exit->B5:IN[Exit] = 000 0000-
OUT[B5] = Us IN[s] = IN[Exit] = 000 0000 defB5 = z = 001 0000useB5 = p = 000 1000OUT[B5] - defB5 = 000 0000IN[B5] = useB5 + (OUT[B5] - defB5) = 000 1000 + 000 0000 = 000 1000
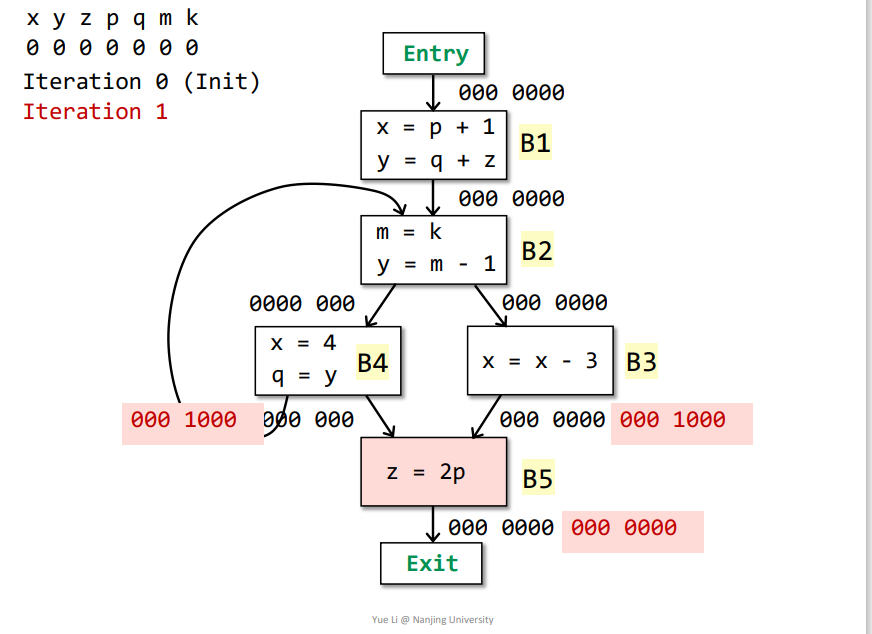
B5->B3:IN[B5] = useB5 + (OUT[B5] - defB5) = 000 0100 + 000 0000 = 000 1000OUT[B3] = Us IN[s] = IN[B5] = 000 1000defB3 = x = 100 0000useB3 = x = 100 0000OUT[B3] - defB3 = 000 1000IN[B3] = useB3 + (OUT[B3] - defB3) = 100 0000 + 000 1000 = 100 1000
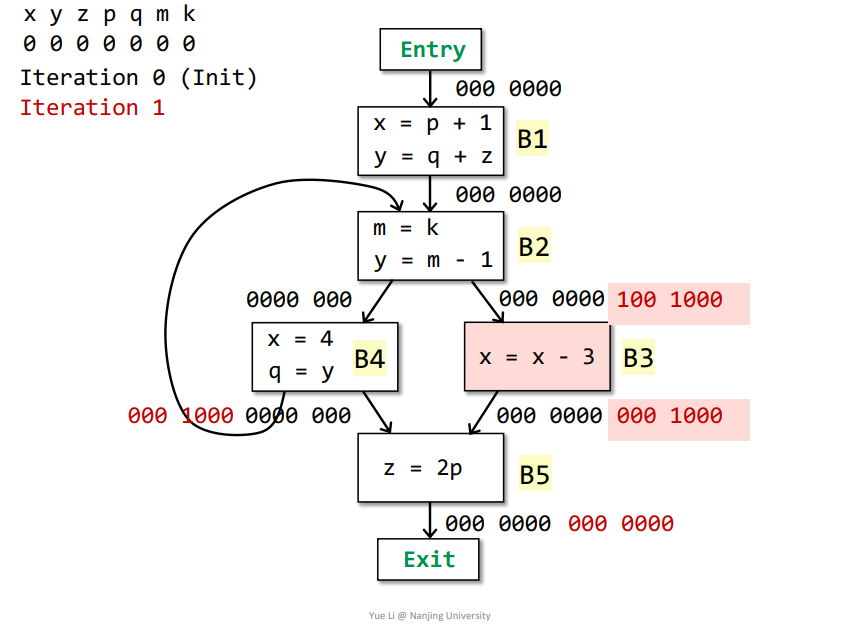
B5->B4:IN[B5] = useB5 + (OUT[B5] - defB5) = 000 0100 + 000 0000 = 000 1000OUT[B4] = Us IN[s] = IN[B5] + IN[B2] = 000 1000 + 000 0000 = 000 1000defB4 = x + q = 100 0100useB4 = y = 010 0000OUT[B4] - defB4 = 000 1000IN[B4] = useB4 + (OUT[B4] - defB4) = 010 0000 + 000 1000 = 010 1000
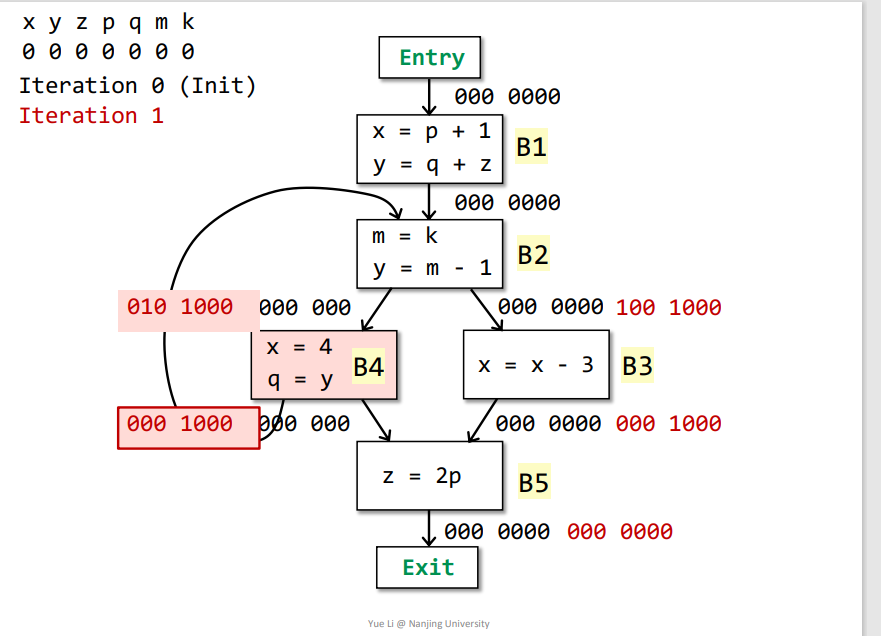
B4、B3->B2:IN[B4] = useB4 + (OUT[B4] - defB4) = 010 0000 + 000 1000 = 010 1000IN[B3] = useB3 + (OUT[B3] - defB3) = 100 0000 + 000 1000 = 100 1000OUT[B2] = Us IN[s] = IN[B3] + IN[B4] = 110 1000defB2 = m + y = 010 0010useB2 = k = 000 0001注意
m是在被使用之前重定义了,所以不能算在useB2中OUT[B2] - defB2 = 100 1000IN[B2] = useB2 + (OUT[B2] - defB2) = 000 0001 + 100 1000 = 100 1001
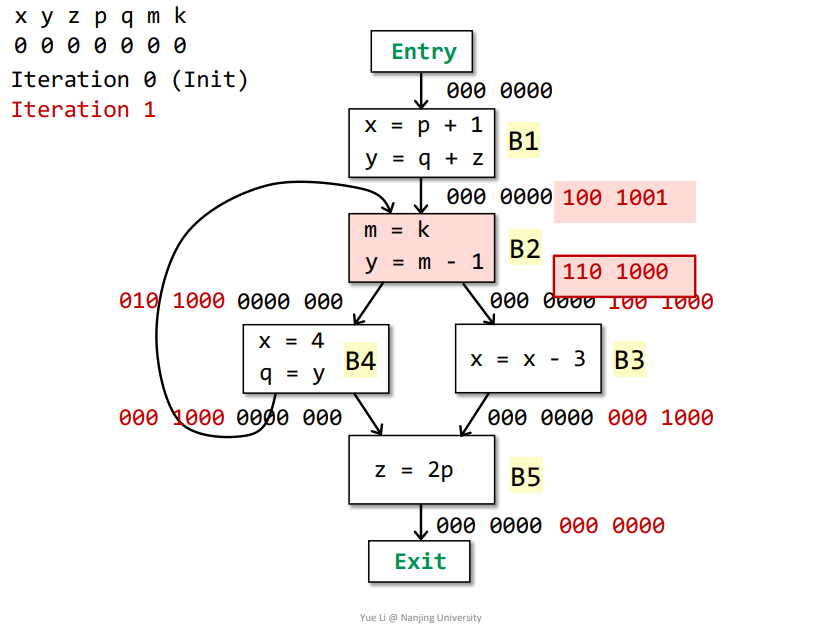
B2->B1:IN[B2] = userB2 + (OUT[B2] - defB2) = 000 0001 + 100 1000 = 100 1001OUT[B1] = Us IN[s] = IN[B2] = 100 1001defB1 = x + y = 110 0000useB1 = p + q + z = 001 1100OUT[B1] - defB1 = 000 1001IN[B1] = useB1 + (OUT[B1] - defB1) = 001 1100 + 000 1001 = 001 1101
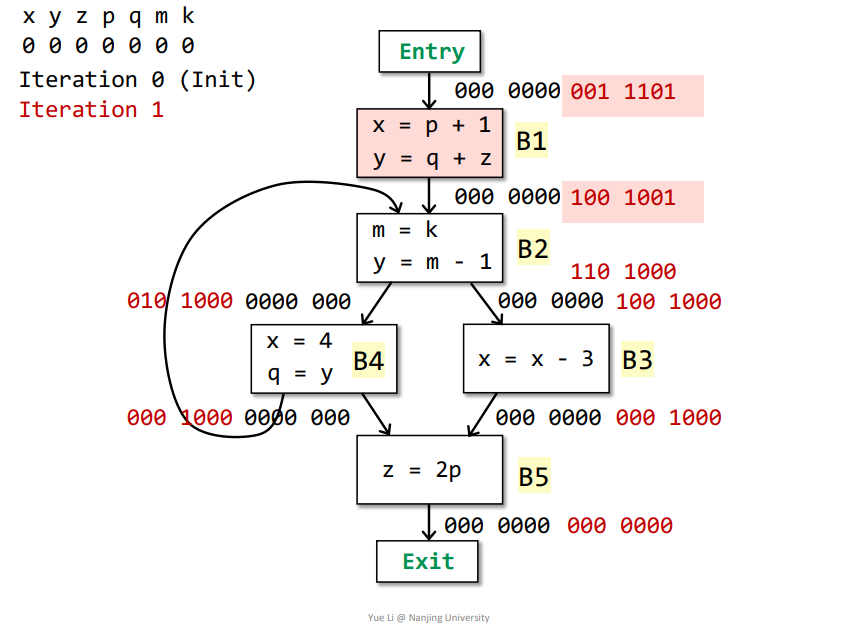
基本块B1、B2、B3、B4、B5的IN[]都发生改变,需要再次迭代,结果如下
第二次迭代
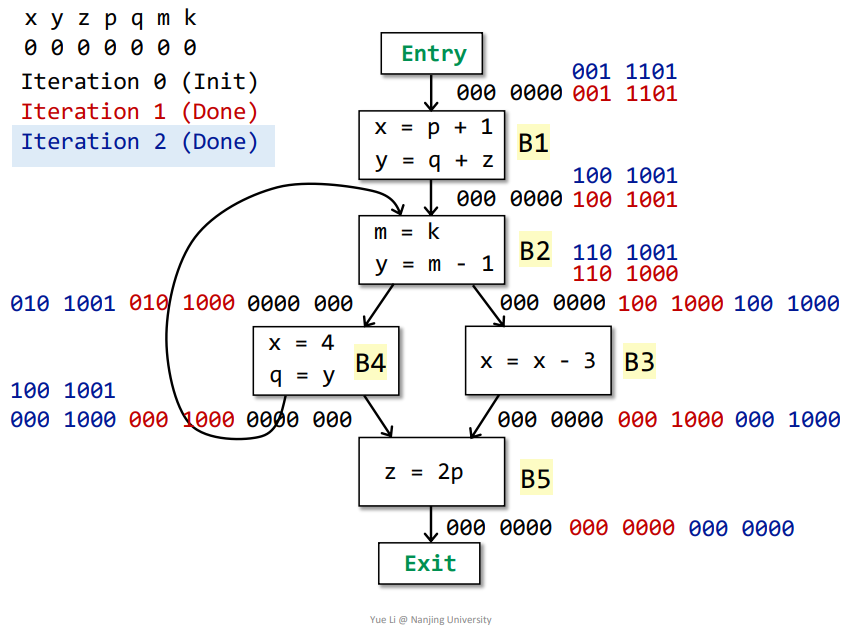
其中B4的IN[]发生改变,需要再次迭代,结果如下
第三次迭代
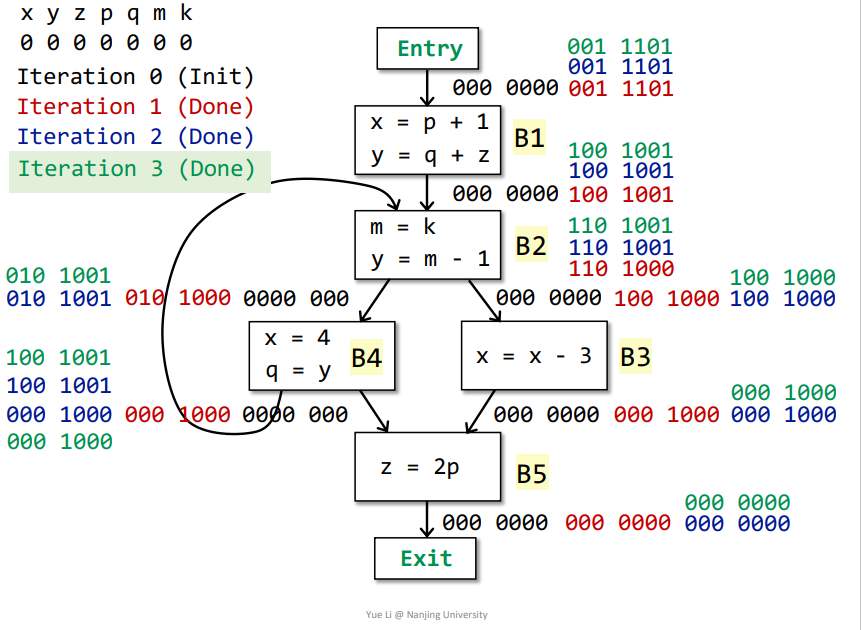
没有基本块的IN[]被改变了,那么不用迭代了
最终含义
同样道理,依据最终结果,比如这里的IN[B3]为100 1000,那么代表在进入基本块B3之前,变量x、p是存活的,在之后的流程中会用到,其他变量在之后的流程不会用到,为dead变量
2.Available Expressions Analysis
概念
一个表达式
x op y如果说在在p点是available的话,那么满足如下条件:所有从
entry到p的路径都会计算表达式x op y在最后一次计算表达式
x op y之后,到p之前,没有再重新定义变量x或者y
应用
- 可以将一个
available的表达式x op y的计算结果,替换成上一次计算表达式x op y的结果,使得不再重复计算 - 用来检测全局公用的子表达式
- 可以将一个
类型:
- 属于是
must analysis,一旦分析出结果,代表该结果一定正确,一定是为available
- 属于是
Data Flow Facts
和之前类似,将所有表达式都用bit向量表示,为1代表available

Control Flow
forward中求IN[B]

1 | IN[B] = ∩p predecessor of B OUT[p] |
即为∩p求基本块B所有前驱的OUT[p]的交集
Transfer Function
为forward,知道IN[B]用来求OUT[B]
$$
OUT[B] = gen_B\ U\ (IN[B] - kill_B)
$$
genB:当前基本块中用到的表达式killB:所有在IN[]中的表达式的变量参与进基本块B中重新定义的表达式合集比如基本块
a = x op y,其中IN[B]为a + b,那么由于IN中变量a在基本块B中重新定义了,所以将IN[B]中关于变量a的表达式都加入到killB中
Algorithm

这里的除了entry外,其他基本块都初始化为top,即1111..111,因为就算有个表达式没有找出来,那就只是代表少优化一次,不影响程序本身的运行流程
例子
如下所示,初始化之后即可开始迭代
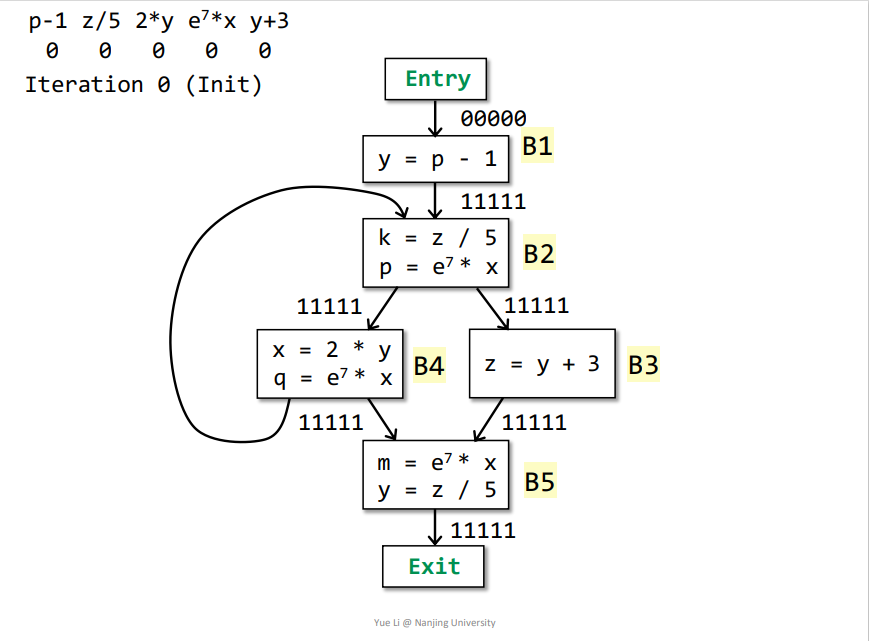
第一次迭代
Entry->B1:OUT[Entry] = 00000IN[B1] = ∩p predecessor of B OUT[p] = OUT[Entry] = 00000genB1 = p-1 = 10000killB1 = 00000IN[B1] - killB1 = 00000OUT[B1] = genB1 + (IN[B1] - killB1) = 10000
B1->B2:OUT[B1] = 10000IN[B2] = ∩p predecessor of B OUT[p] = OUT[B1] ∩ OUT[B4] = 10000 ∩ 11111 = 10000genB2 = z/5和e^7*x = 01010killB2 = p-1 = 10000IN[B2] - killB2 = 00000OUT[B2] = genB2 + (IN[B2] - killB2) = 01010
B2->B3:OUT[B2] = 01010IN[B3] = ∩p predecessor of B OUT[p] = OUT[B2] = 01010genB3 = y+3 = 00001killB3 = 01000其中
z在IN[B3]中有表达式z/5用到,那么需要将对应表达式加入到killB3集合中IN[B3] - killB3 = 00010OUT[B3] = genB3 + (IN[B3] - killB3) = 00011
B2->B4:OUT[B2] = 01010IN[B4] = ∩p predecessor of B OUT[p] = OUT[B2] = 01010genB4 = 2*y和e^7*x = 00110killB4 = 00010IN[B4] - killB4 = 01000OUT[B4] = genB3 + (IN[B4] - killB4) = 01110
B3、B4->B5:OUT[B3] = 00011OUT[B4] = 01110IN[B5] = ∩p predecessor of B OUT[p] = OUT[B4] ∩ OUT[B3] = 00010genB5 = e^7*x和z/5 = 01010killB5 = 00000IN[B5] - killB5 = 00010OUT[B5] = genB5 + (IN[B5] - killB5) = 01010
基本块B1、B2、B3、B4、B5的OUT[]都发生改变,需要再次遍历
第二次迭代
同理可得,结果如下
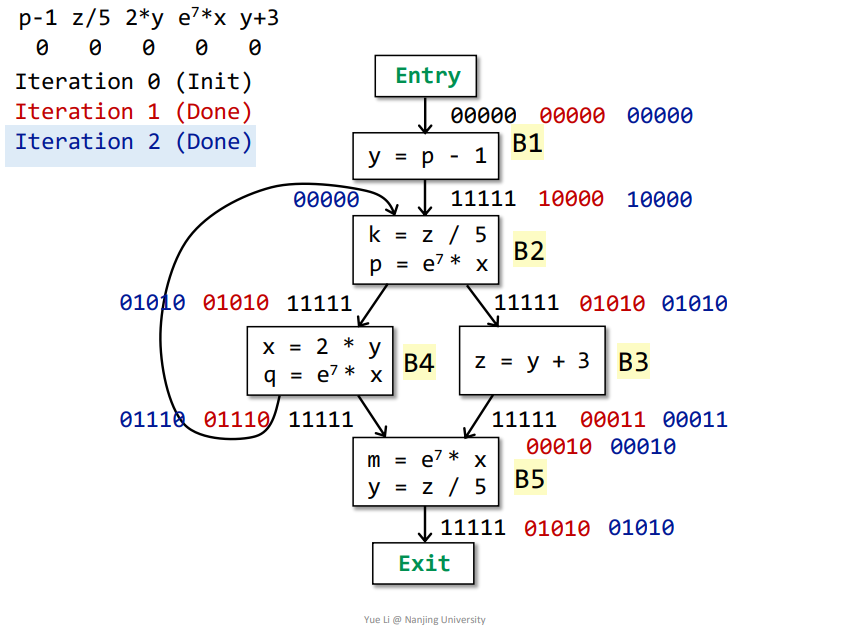
没有基本块的OUT[]发生改变,可为最终结果
最终含义
依据最终结果,拿基本块B2而言,对于表达式e^7*x是available的,那么在程序第一次经过B2时,由于表达式e^7*x还没被计算,那么先计算,然后保存。当通过循环第二次经过B2时,其表达式e^7*x就可以被直接替换为上一次表达式的值,在这里也就是在基本块B4中得到的值,其他的同理可得。
3.Data Flow Analysis总结
异同
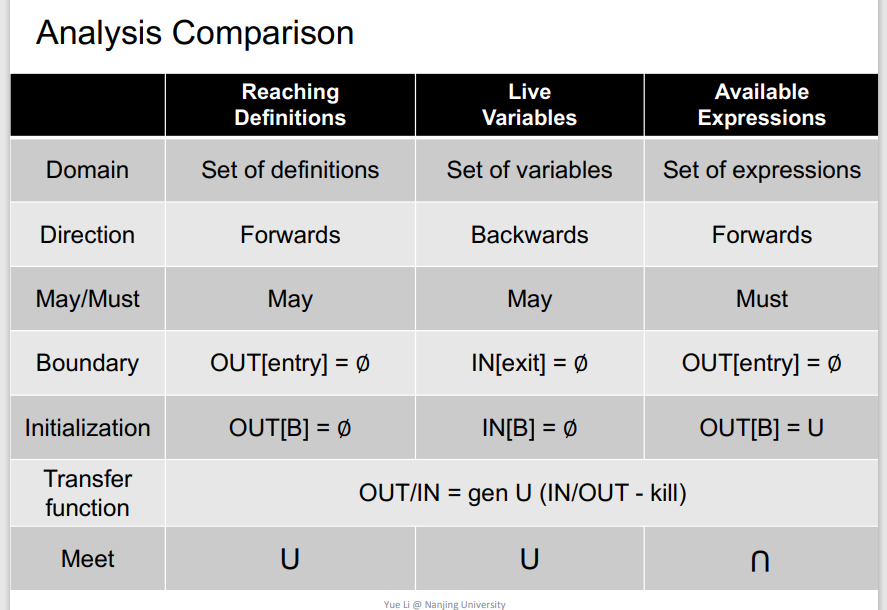
需要掌握的

三种数据流分析算法、异同以及为什么迭代算法可以停止
停止的原因就是迭代到最后,最差的情况就是全是top:1111..或者全是bottom:0000....
四、Data Flow Analysis - Foundations I

1.偏序(Partial Order)
poset偏序集
性质:
$$
\begin{align}
&\forall x \in P,x\subseteq x\quad &(Reflexivity)\
&\forall x,y \in P,x\subseteq y ∧ y\subseteq x =>x=y\quad &(Antisymmetry)\
&\forall x,y,z\in P,x\subseteq y ∧ y\subseteq z =>x \subseteq z \quad &(Transitivity)
\end{align}
$$
2.Upper and Lower Bounds
$$
u\in P,u\ is \ an \ upper\ bound\ of\ S,if\ \forall x\in S,x\subseteq u\
l\in P,l\ is \ an \ lower\ bound\ of\ S,if\ \forall x\in S,l\subseteq x\
$$
lub/join(least upper bound)lub定义符号为⊔S,满足⊔S ⊑ u,u为上界glb/meet(greatest lower bound)glb定义符号为⊓S,满足l ⊑ ⊓S,如果
S ⊑ P(P,⊑),并且S只有两个元素,假定为S={a,b},那么可得如下⊔S = a⊔b (join)⊓S = a⊓b (meet)
不是所有偏序集都有最大下界或者最小上界
如果一个偏序集有最大下界或者最小上界,那么一定是唯一的
3.Lattice
Lattice(格)
如果一个偏序集中任意两个元素组成一个集合,都有最小上界和最大下界存在,那么该偏序集即为一个lattice
P(P,⊑), ∀a,b∈P, a⊔b and a⊓b exists => P is a lattice
Semilattice(半格)
如果一个偏序集中任意两个元素组成一个集合,最小上界和最大下界中只有一个存在,那么该偏序集即为一个Semilattice
join semilattic:a⊔b存在,a⊓b不存在meet semilattic:a⊓b存在,a⊔b不存在
Complete Lattic(全格)
定义:
如果对于一个偏序集中任意一个子集,都有最小上界和最大下界存在,那么该偏序集即为一个Complete Lattice
每一个全集都有一个最大元素和最小元素
- 最大元素
(a greatest element T) = ⊔P = top - 最小元素
(a least element ⊥) = ⊓P = bottom
性质:
所有有限的Lattice都是Complete Lattic,但是一个Complete Lattic不一定是有限的,比如0-1这个偏序集中所有实数(包括0,1)作为一个集合,存在边界,是一个Complete Lattic,但是里面的子集的元素就可以是无限的。
Product Lattice
一个Lattice合集,其中所有Lattice都由最小上界和最大上界,那么即可称该Lattice合集为一个Product Lattice
4.Fixed-Point
Monotonicity(单调)
对于一个Lattice L,有函数f:∀x∈L,f(x)∈L,假定该函数存在单调性,则L满足单调
1 | ∀x,y∈L,x⊑y => f(x)⊑f(y) |
🔺mark:那单调性怎么证明呢?
Fixed-Point Theorem(不动点理论)
给定一个Complete Lattice L,L满足单调且有限,那么可以用来求不动点
最小不动点
含义
$$
f(⊥),f(f(⊥)),…..,f^k(⊥)会达到最小不动点
$$
证明
首先是存在不动点证明
$$
\begin{align}
&\because\forall x,y\in L,x\subseteq y => f(x)\subseteq f(y)(Monntonicity)\
&\therefore⊥\subseteq f(⊥)\
&\therefore f(⊥)\subseteq f(f(⊥)) = f^2(⊥)\
&\therefore ⊥\subseteq f(⊥) \subseteq f^2(⊥)\subseteq …\subseteq f^i(⊥)\
&\because L\ is\ finite\
&\therefore f^{Fix} = f^k(⊥) = f^{k+1}(⊥)
\end{align}
$$然后是证明求得的不动点是最小不动点,还是不太理解提到的数学归纳法,既然从
⊥开始做f,那么到某个k就必定存在不动点,那么将x也做k个f不就好了吗。假定存在其他的不动点
x,那么有x = f(x),⊥⊑x
$$
\begin{align}
&\because\forall x,y\in L,x\subseteq y => f(x)\subseteq f(y)(Monntonicity)\
&\therefore f(⊥)\subseteq f(x)\
&\therefore f^2(⊥)\subseteq f^2(x)…f^i(x)\subseteq f^i(x)\
&\because \exist k,f^k(⊥) = f^{Fix}\
&\therefore f^{Fix} = f^k(⊥) \subseteq f^k(x)=x\
\end{align}
$$
那么就代表通过⊥求得的不动点一定是最小不动点,这里和李樾老师不一样,我也不知道能不能这么写,老师原版是数学归纳法induction
最大不动点
含义
$$
f(T),f(f(T)),…..,f^k(T)会达到最大不动点
$$
证明
证明和最小不动点证明类似
5.应用
这里把老师上课讲的放到最后了
理论应用
即依据Lattice的定义,将之前提到的算法中
需要求的所有的
OUT/IN当作一个元素V(111..0000...),依据相关性质可知道该元素V为一个Complete Lattice,任意子集都有最大下界和最小上界,并且finite
$$
&OUT[B_1]&OUT[B_2]&…&OUT[B_n]\
&V_1 &V_2&…&V_n
$$将
Transfer function作为刚刚提到的给定的f函数,其单调性需要证明,**(这里好像还没有证明)**那么每迭代一轮,就相当于对所有的IN/OUT做一次Transfer function。将每一次迭代结果合并为一个集合
Xi,可知该集合为一个Product Lattice,此外该Product Lattice Xi(finite)中所有元素均为一个Complete Lattice,那么该Xi也是一个Complete Lattice,然后加入Transfer function可得如下结果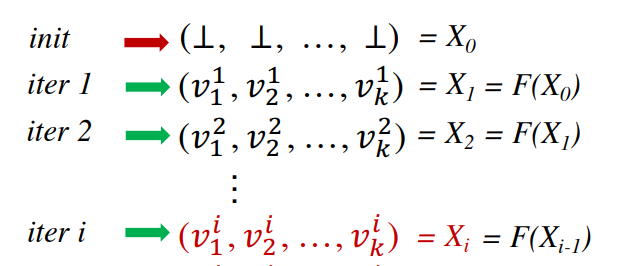
那么即可用到Fixed-Point Theorem(不动点)理论来求最终结果,回答如下问题
问题

- 算法是否能够确保有解,可达不动点?
- 是否只有一个不动点,通过算法求解得到的不动点是否是最好的?
- 什么时候可以达到不动点?
🔺mark:好像后面两个问题还没有解决
五、Data Flow Analysis - Foundations II

1.Prove Function F is Monotonic
分析:
一般而言F形式为OUT/IN = gen ⊓/⊔ (IN/OUT - kill)
由于对于每一个基本块BB而言,gen和kill都是固定的,即为单调的常数,所以这里的需要证明的就是⊓/⊔是否为单调的,先证明⊔为单调,证明方法对⊓同理
证明如下:
⊔定义:求任意两个元素的最小上界
想要证明⊔为单调,即转化为证明如下结论
$$
\forall x,y,z\in L,x\subseteq y\ =>\ x⊔z\subseteq y⊔z
$$
证明过程:
$$
\begin{align}
&\therefore y⊔z\ is\ an\ least\ upper\ bound\ of\ y\
&\therefore y\subseteq y⊔z\
&\because x\subseteq y\
&\therefore x\subseteq y⊔z\ =>\ y⊔z\ is\ an\ upper\ bound\ of\ x \
&\because x⊔z\ is\ an\ least\ upper\ bound\ of\ x\
&\therefore x⊔z\subseteq y⊔z
\end{align}
$$
证毕
那么即可得到对于每一个基本块的Function F是单调的,由于每次迭代的时候的f即代表对每一个基本块做Function F,所以f也是单调的。
2.Time Complexity
即什么时候到达不动点
偏序集高度
h定义,从Top到Bottom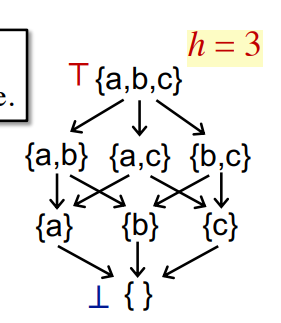
那么一个算法中有个k个node,最坏情况就是,每次迭代,只有一个node的一个bit从0->1。而bit的数量其实就是偏序集的高度h,从而得到最坏的情况就是迭代h*k次,从而把所有node的所有bit都从0->1,时间复杂度即为h*k。
3.May and Must Analyses,a Lattice View
将一个Lattice抽象称一个图形,如下
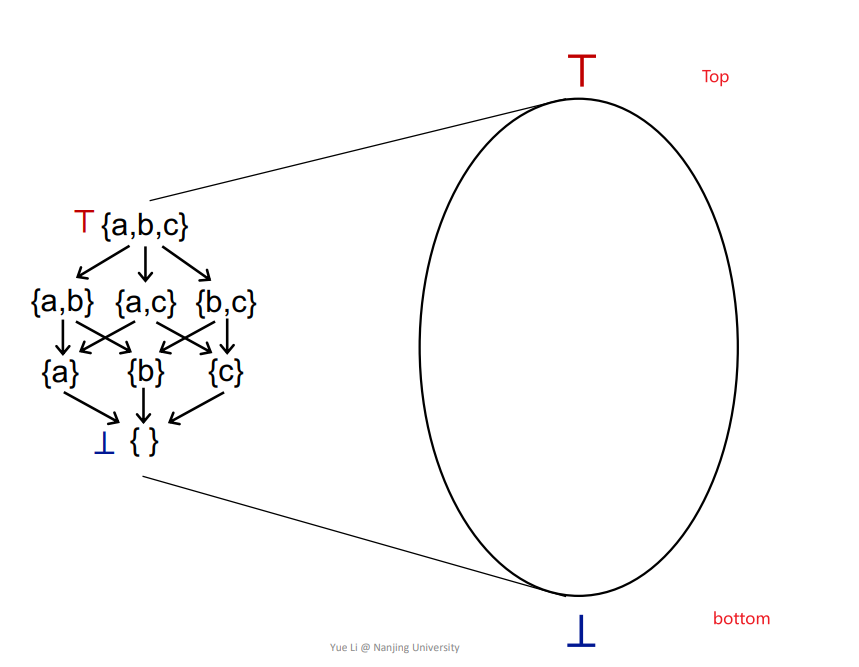
May Analysis/Must Analysis基本都是从unsafe->safe的过程,也就是safe-approximation主要就是如下的图
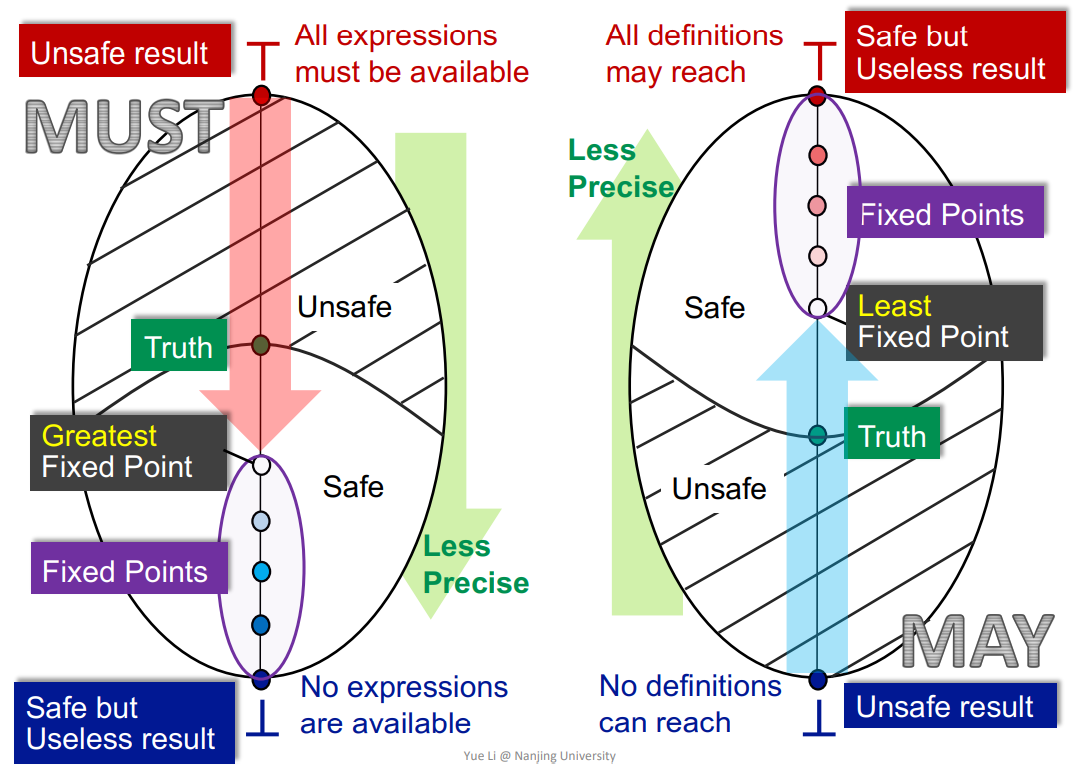
May:- 从
Bottom->Top,从不准确到准确,达到Least Fixed Point。 - 比如
Reaching Definition,unSafe就是No definitions can reach到safe,也就是All definitions may reach的过程。
- 从
Must:- 从
Top->Bottom,也是从不准确到准确,达到Greatest Fixed Point。 - 比如
Expressions available,它的safe就必须是No expressions are available。因为误报了一个expression是available的话,那么整个程序优化之后就会出错,所以它的safe只能是No expressions are available,然后即可推得其他的。
- 从
大概是懂了,但是如果再来设计一个算法,是依据什么原则或者什么方法来将它设计成Must还是May呢。
比如活跃变量分析,其应用通常是用来提高寄存器利用率的,用来求dead变量的,就算求不出来dead变量,其实对程序实际的运行结果并不会造成影响,所以应该设计成May。但是能不能设计成Must呢?设计成Must是会出错,还是会导致优化程度不够高呢,好像是后者把。
4.How Precise Is Our Solution
Meet-Over-All-Paths Solution(MOP)
即所有从Entry到该某点Si的Path的一些运算
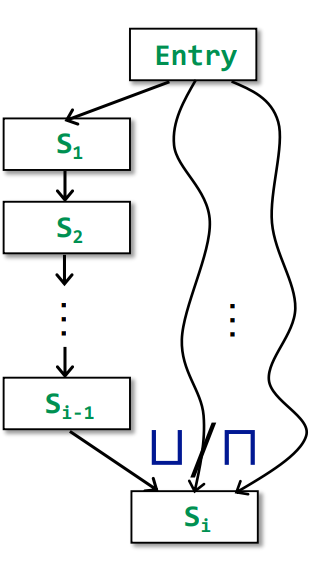
1 | MOP[Si] = ⊔/⊓ Fp(OUT[Entry]) |
其中Fp代表从Entry到Si某条路径的所有Transfer funstion的一个集合函数。比如有一条路径为Entry->S1->S2->...->Si,那么整条路径从Entry->Si-1可得OUT[Si-1] = Fp(OUT[Entry])
MOP[Si]即求所有路径(当然不同路径的Si-1可能不同)到Si的一个meet/join,也就是将不同路径的OUT[Si-1]做一个meet/join操作。
有些Path在实际的动态运行过程中可能不存在,但是在静态分析时会将之归入进来计算。
MOP vs Ours(Iterative Algorithm)
假定如下情况
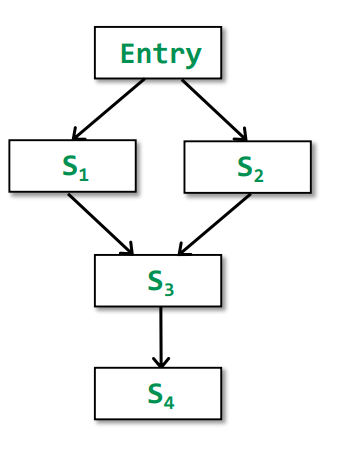
依据定义可分别得到对应的结果
$$
\begin{align}
&Ours[S4]=IN[S4]=f_{s3}(f_{s1}(OUT[Entry])⊔f_{s2}(OUT[Entry]))\
&MOP[S4]=IN[S4]=f_{s3}(f_{s1}(OUT[Entry]))⊔f_{s3}(f_{s2}(OUT[Entry]))
\end{align}
$$
其中fs1(OUT[Entry])和fs2(OUT[Entry])是一样的,那么将之抽象为x和y,fs3抽象为F可得简化后的结果
1 | Ours = F(x⊔y) |
证明一下两者的关系
$$
\begin{align}
&\therefore x\subseteq x⊔y\ and\ y\subseteq x⊔y\
&\because ∀x,y\in L,x\subseteq y => F(x)\subseteq F(y)(Monotonic)\
&\therefore F(x)\subseteq F(x⊔y)\ and\ F(x)\subseteq F(x⊔y)\
&\therefore F(x⊔y)\ is\ an\ upper\ bound\ of\ F(x)\ and\ F(y)\
&\because F(x)⊔F(y)\ is\ an\ least\ upper\ bound\ of\ F(x)\ and F(y)\
&\therefore F(x)⊔F(y)\subseteq F(x⊔y)\
&\therefore MOP\subseteq Ours
\end{align}
$$
又因为如下关系图

在may analysis中,越接近上界越不准确,所以Ours比MOP更加不准确
但是如果满足Transfer function F 是distributive(可分配的),即分配律,那么可得F(x⊔y) = F(x)⊔F(y)的,那么MOP=Ours。即当Transfer function是可分配的,即代表MOP其实是等价于Ours的。
有个结论:
Bit-vector or Gen/Kill problems (set union/intersection for join/meet) are distributive
就是前面提到的关于Bit-Vector方法定义的,或者是Gen/Kill定义的Transfer function都是可以分配的
5.Constant Propagation
使用的是MOP
Data Flow Facts
将所有的变量是否为常量都表达为一个组合pairs,即(x,v),也就是当前经过node之后的OUT中该变量x的值v
Control Flow
和Expression Analysis一样,应该是Must的,因为safe的时候,应该是所有变量都不是常量,对应在Bottom,也就是NAC(Not an constant)。而由于是组合键值pair形式,所以Top应该是undefine,也就是UNDEF形式,最终如下
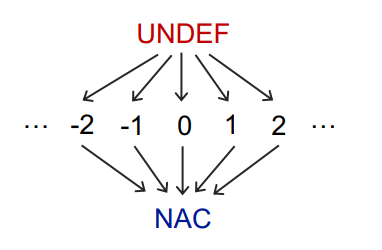
然后需要设计一下Meet操作,表达式同样类似
1 | IN[B] = ⊓p predecessor of B OUT[p] |
一个变量v与另一个进来的值对应的无非如下几种情况
v ⊓ UNDEF = v没定义的碰见另一个,当然直接相当于另一个了
v ⊓ NAC = NAC既然已经确定不是常量,那么无论另一边值是啥,该变量必定不是常量了
v ⊓ constantc ⊓ c = c两边均为常量才是常量
c1 ⊓ c2 = NAC两边值不同就不是常量了
UNDEF ⊓ c = c(和前面一样)NAC ⊓ c = NAC(和前面一样)
Transfer Function
1 | F: OUT[s] = gen⊔(IN[s] - {(x, _)}) |
即需要去掉所有其他node中关于变量x的键值对pair,然后加上当前生成的变量键值对pair。
使用函数val(x)来求对应x的值,然后对应不同的statement有如下情况
s : x = constant;s : x = y;s : x = y op z;f(y,z) = val(y) op val(z) //val(y)和val(z)都是常量时f(y,z) = NAC //val(y)或者val(z)有一个是NAC时f(y,z) = UNDEF //其他情况
是一个Nondistributivity,例子如下
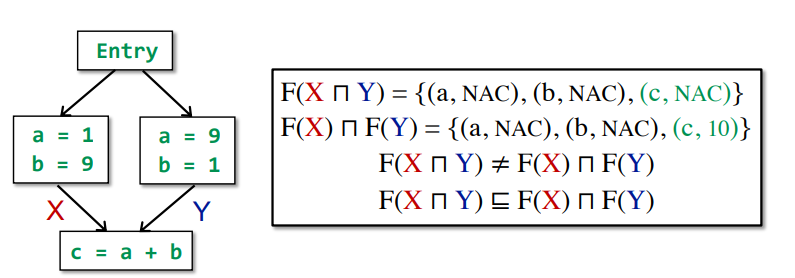
Worklist Algorithm
一个Iterative Algorithm的优化算法

Iterative Algorithm只要变化了一个,其他的都会重新计算,而Worklist Algorithm是只计算当前轮次变化的OUT[B]以及后续的OUT[B],相当于用空间换取时间。
原因就是一个Transfer function,IN[]没有变,那么OUT[]肯定也是没有变。
主要是图中黄色的部分,相比于Iterative Algorithm是有些改变的。
Foundations总结

Iterative algorithm、Lattice定义、不动点理论、may/must分析、MOP和Iterative algorithm的异同比较、常量分析、Worklist algorithm
六、Interprocedural Analysis

之前学的都是过程内分析intraprocedural analysis,接下来要学习过程间分析Interprocedural Analysis,即函数调用的相关分析
1.Motivation
如果不进行相关的Interprocedural Analysis,那么当遇到函数调用时,通常解决办法都是safe-approximation,也就是将之判定为一个safe地方的Facts。比如对于Constant Analysis而言,就会函数调用返回的结果判定为NAC,更加安全。
一些定义:
如下所示,在函数之前存在相关的call edges,以及return edges

2.Call Graph Construction
定义
调用图是程序中一个函数调用边call edges集合,比如如下所示,左边为程序,右边即为它的调用图
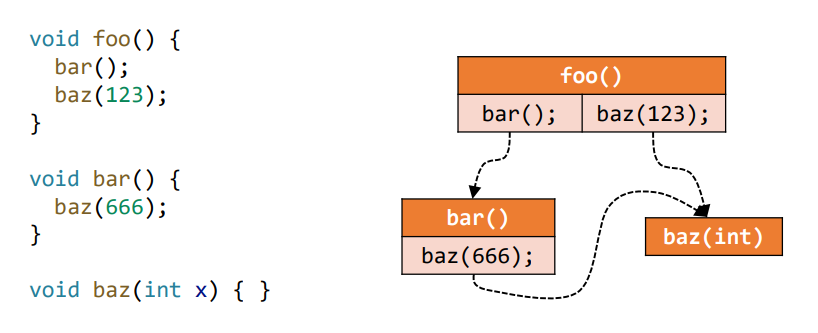
面向对象语言调用图常见算法

3.Method Calls (Invocations) in Java
在JAVA中通常存在三种调用方法,而在JAVA8中还引入了invokedynamic,这个是特殊用途,不讨论
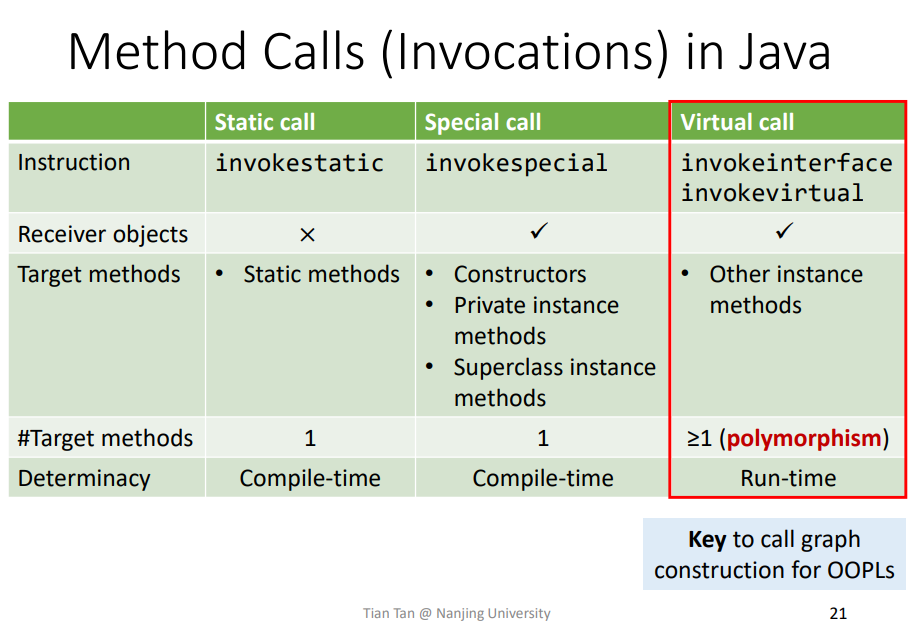
主要是对于Vitual call,一个调用由于传入的对象不同,可能对应不同的方法。这个是实现OO(Object-Oriented)语言中多态polymorphism的关键点,也是静态分析中的难点。
Method Dispatch of Vitual Calls
定义
即程序运行时动态求解Vitual Calls动态函数方法的过程,就叫做Method Dispatch,求解一般需要以下两个要素
- 传入对象的类型
- 函数签名,
call site不知道啥意思Signature = class type + method name + descriptordescriptor = return type + parameter types
Dispatch Function Defination
依据Method Dispatch定义来确定对应方法定义
c:即class,传入对象的类型m:即函数签名

Dispatch是寻找可以调用的函数,那么可以调用的函数一定是要确保该函数是有具体的函数体的,不能是抽象的non-abstract
例子

Dispatch(B,A.foo()):先从B中找,找不到就找父类,也就是A,从A中获取到foo函数。Dispathc(C,A.foo()):先从C中找,直接找到,那么即为c中的foo函数。
4.Class Hierarchy Analysis(CHA)
- 需要一个类的相关继承结构
- 求解一个
vitural call依据于定义类型和传入的对象
Call Resolution of CHA
定义方法Resolve(cs)为具体算法分析实例

其中
cs: 当前分析的语句m: 函数签名c^m:m对应的类型
具体分析一下
static call
例子如下
1 | class C{ |
可得对应变量含义
$$
\begin{align}
&cs : C.foo(x,y); &//当前需要方法解析语句\
&m : <C: T\ foo(P,Q)> &//函数签名\
\end{align}
$$
直接返回了对应函数签名的m
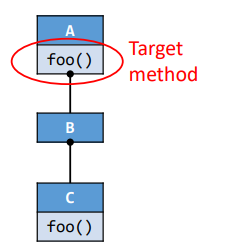
speciall call
superclass instance methods
1 | class C extends B{ |
可得对应变量含义
$$
\begin{align}
&cs:super.foo(p,q);\
&m:<B: T\ foo(P,Q)>\
&c^m:B
\end{align}
$$
由于是super,所以对应对象类型为B。同时需要注意的是这里不能把super直接替换为B,因为可能B中没有定义foo函数,而是在其父类中定义,如下
Constructors/Private instance mthods
这两个可以放到一起
1 | Class C extends B{ |
对应变量含义
$$
\begin{align}
&cs:this.bar();\
&m:<C:T\ bar()>\
&c^m:C\
\
&cs:C\ c\ =\ new\ c();\
&m:<>
\end{align}
$$
这个可以直接找到,不细说
vitural call
1 | class A{ |
对应变量含义
$$
\begin{align}
&cs:a.foo(x,y);\
&m:<A:\ T\ foo(P,Q)>\
&c:A\
\end{align}
$$
其中关于该算法

需要遍历c的所有直接子类以及间接子类,通过Dispatch进行计算,将计算记过放入T中
实际例子
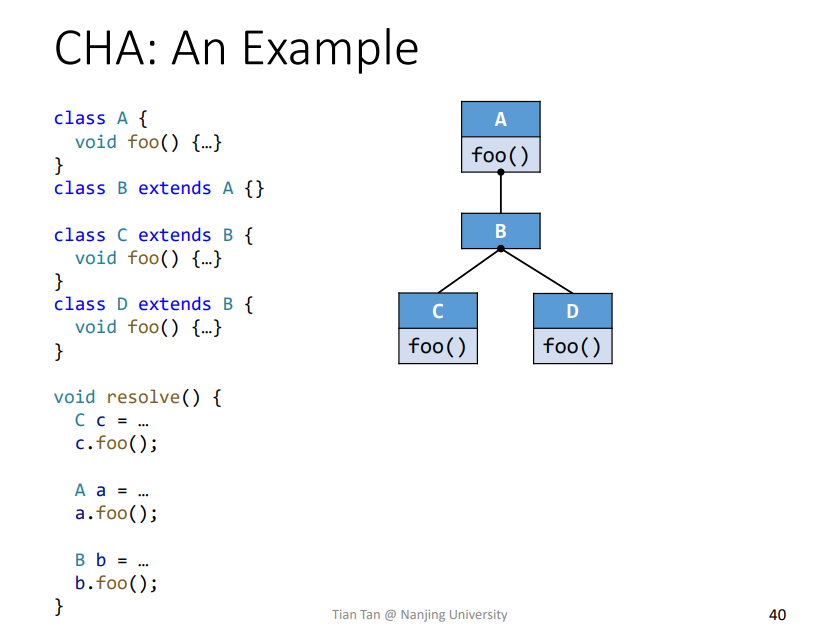
1 | Resolve(c.foo()) = {C.foo()} |
关于Resolve(b.foo())计算结果,前面提到dispatch算法,当在当前类,这里也就是B中没有找到对应函数foo定义,就会去其父类寻找,这里也就是A,所以实际执行进入循环体的类为A,那么其结果就相当于Resovle(a.foo())了。
Features of CHA
Advantage
很快,只考虑声明类型,然后查找继承树。求解过程中忽略数据流和控制流的相关信息。
Disadvantage
不准确,因为忽略了数据流和控制流的相关信息
Algorithm

主要是从Work list中取方法后,需要先判断是否已经reachable了,即是否在RM中
例子

首先初始化如下
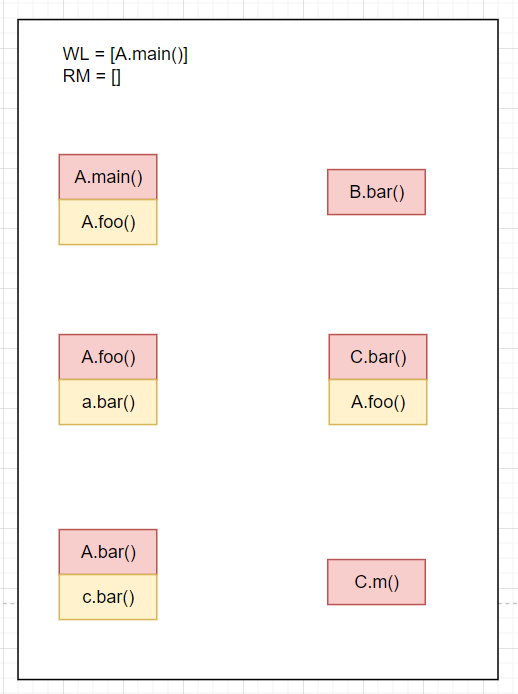
WL=[A.main()],RM=[],CG=[]从
WL取出A.main(),不属于RM,则放入RM,RM=[A.main()]A.main的call site为A.foo()求解
Resolve(A.foo()),利用之前的提到的Resolve算法,求解得到A.foo(),放入WL中,并且相关边放入CG结果如下
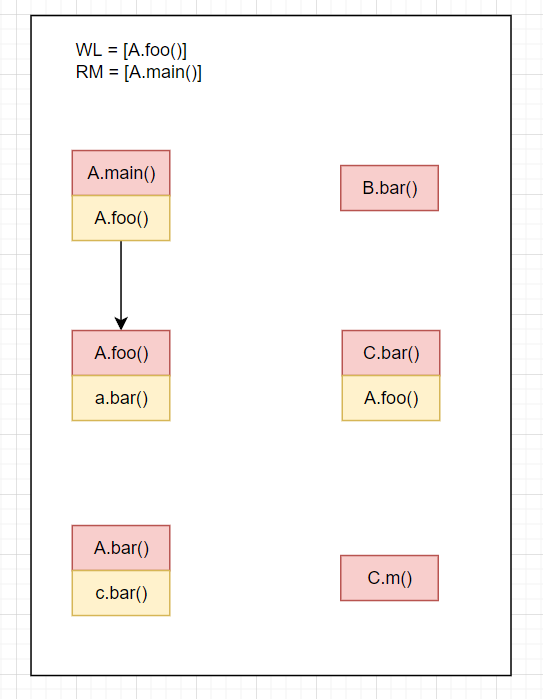
WL=[A.foo()],RM=[A.main()],CG=[A.main().A.foo()->A.foo()]RM=[A.main(),A.foo()]Resolve(cs of A.foo()) = Resolve(a.bar()) = A.bar()+B.bar()+C.bar(),A.foo().a.bar()->[A.bar,B.bar,C.bar()]放入CGWL=[A.bar(),B.bar(),C.bar()]结果如下
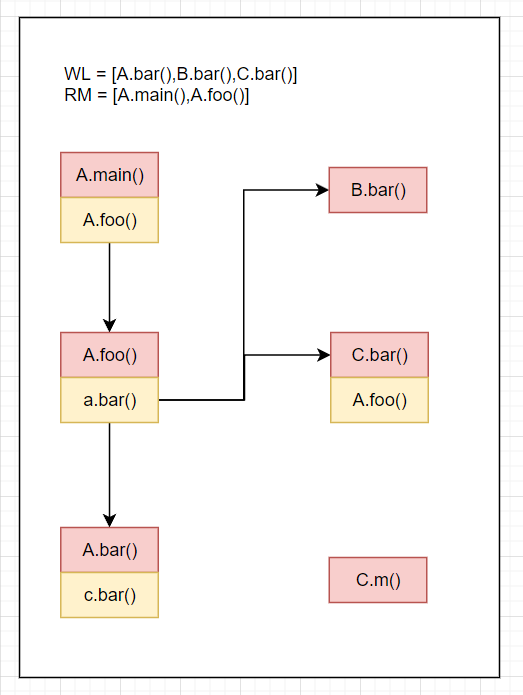
WL=[A.bar(),B.bar(),C.bar()],RM=[A.main(),A.foo()],CG=[A.main().A.foo()->A.foo(),A.foo().a.bar()->{A.bar(),B.bar(),C.bar()}]RM=[A.main(),A.foo(),A.bar()]Resolve(cs of A.bar()) = Resolve(c.bar()) = C.bar(),A.bar().c.bar()->C.bar()放入CGWL=[B.bar(),C.bar(),C.bar()]结果如下
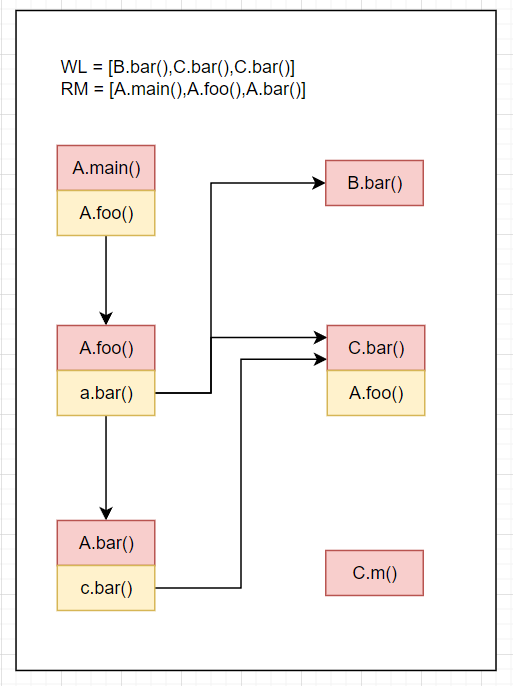
WL=[B.bar(),C.bar(),C.bar()],RM=[A.main(),A.foo(),A.bar()],CG=[A.main().A.foo()->A.foo(),A.foo().a.bar()->{A.bar(),B.bar(),C.bar()},A.bar().c.bar()->C.bar()]RM=[A.main(),A.foo(),A.bar(),B.bar()]Resolve(cs of B.bar()) = Resolve() = []WL=[C.bar,C.bar()]结果如下
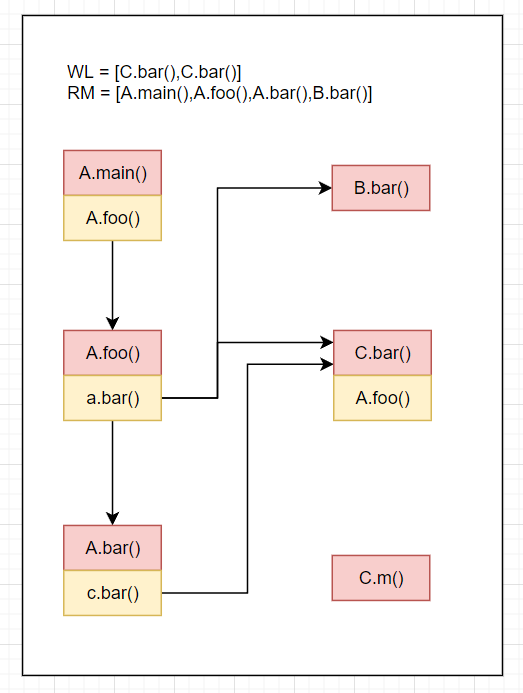
WL=[C.bar(),C.bar()],RM=[A.main(),A.foo(),A.bar(),B.bar()],CG=[...]RM=[A.main(),A.foo(),A.bar(),B.bar(),C.bar()]Resolve(cs of C.bar()) = Resolve(A.foo()) = A.foo(),C.bar().A.foo()->A.foo()放入CGWL=[C.bar().A.foo()]结果如下
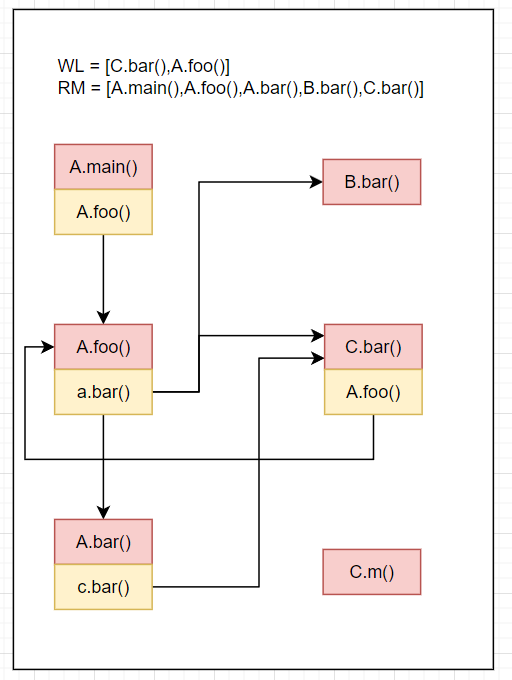
WL=[C.bar(),A.foo()],RM=[A.main(),A.foo(),A.bar(),B.bar(),C.bar()],CG=[A.main().A.foo()->A.foo(),A.foo().a.bar()->{A.bar(),B.bar(),C.bar()},A.bar().c.bar()->C.bar(),C.bar().A.foo()->A.foo()]C.bar()在RM中,跳过,从WL中移除C.bar()结果如下
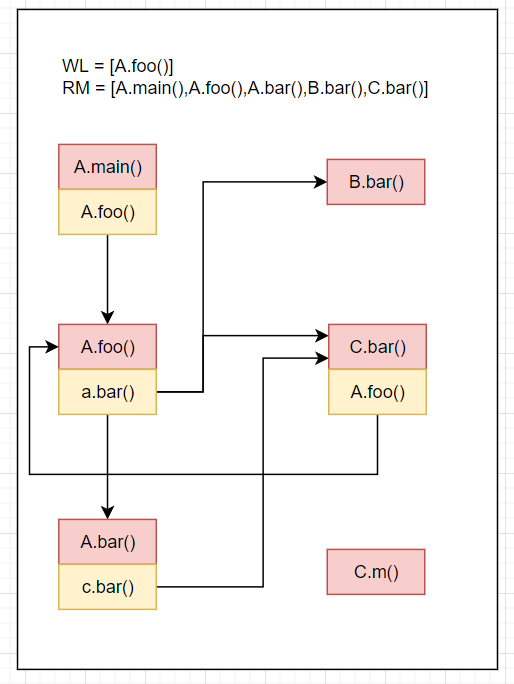
WL=[A.foo()],RM=[A.main(),A.foo(),A.bar(),B.bar(),C.bar()],CG=[...]A.foo()在RM中,跳过,从WL中移除A.foo()结果如下
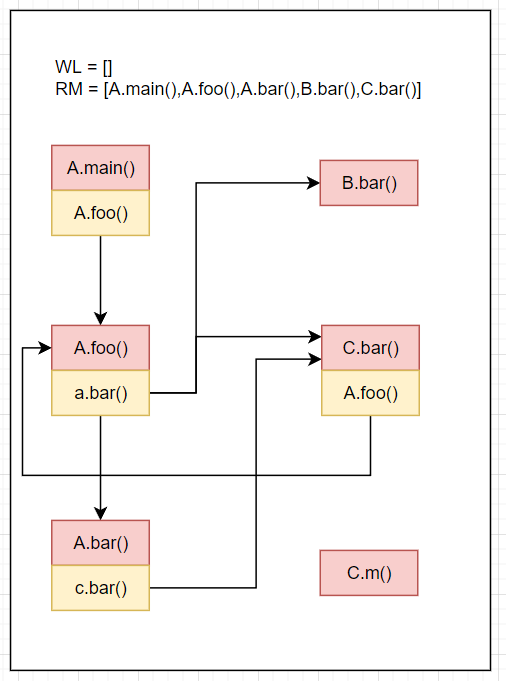
WL=[],RM=[A.main(),A.foo(),A.bar(),B.bar(),C.bar()],CG=[...]WL为空,算法结束。最终结果如下

其中CG的表达形式不知道怎么写合适,就只能大概写一下
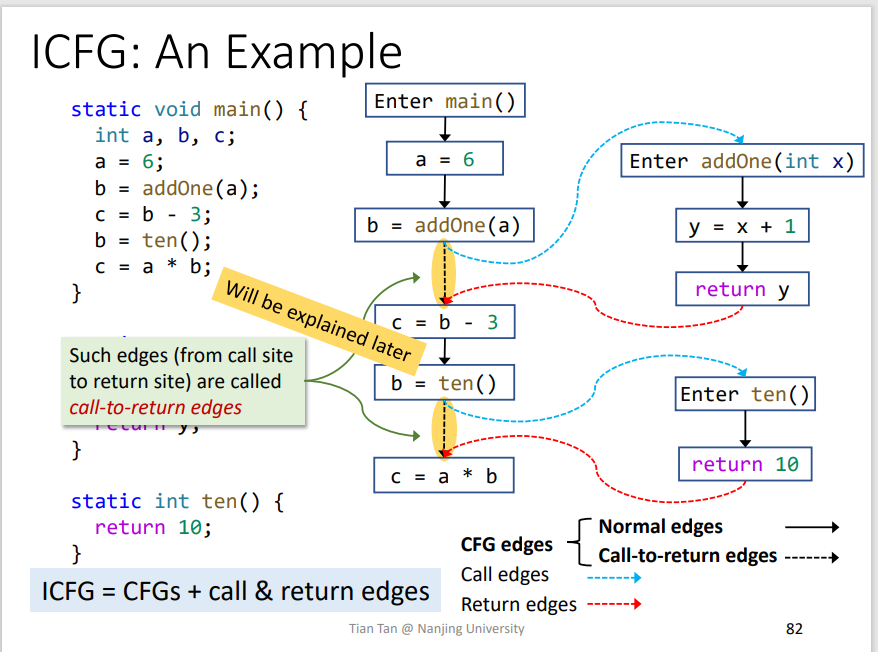
5.Interprocedural Control-Flow Graph
- CGF:展示的是方法之间的调用关系
- ICFG:展示的是整个程序的调用关系
ICFG = CFGs + call&return edgescall edges: 即调用边,call site到对应函数入口点return edges: 即函数返回点到该函数的被调用点
6.Interprocedural Data-Flow Analysis
其实相对于Intraprocedural Data-Flow Analysis,会多call transfer function和return transfer function。即数据进入函数前的转化函数以及回来的时候的转化函数

Interprocedural Constant Propagation
主要是Node transfer,即如下情况,即为一个Node transfer
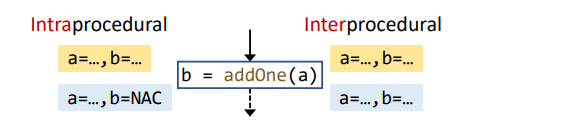
实例
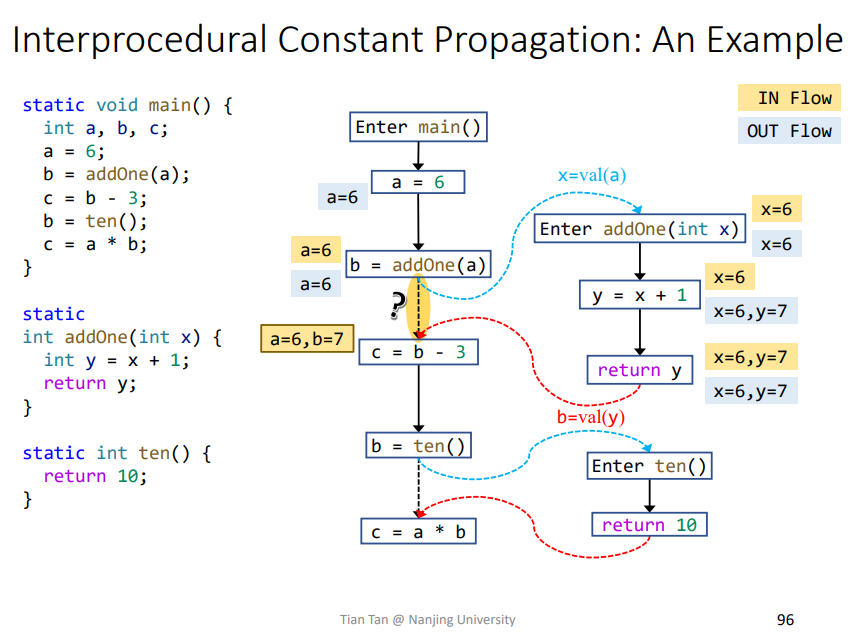
其中打问号的边叫做call-to-return edge,是用来传递本函数变量的,即该函数内部的变量,即这里的a,如果没有的话,就会导致本函数变量的传播经过调用函数绕一大圈才能回来。如下所示,本函数变量a就需要经过addOne传播才能回来,很影响效率。
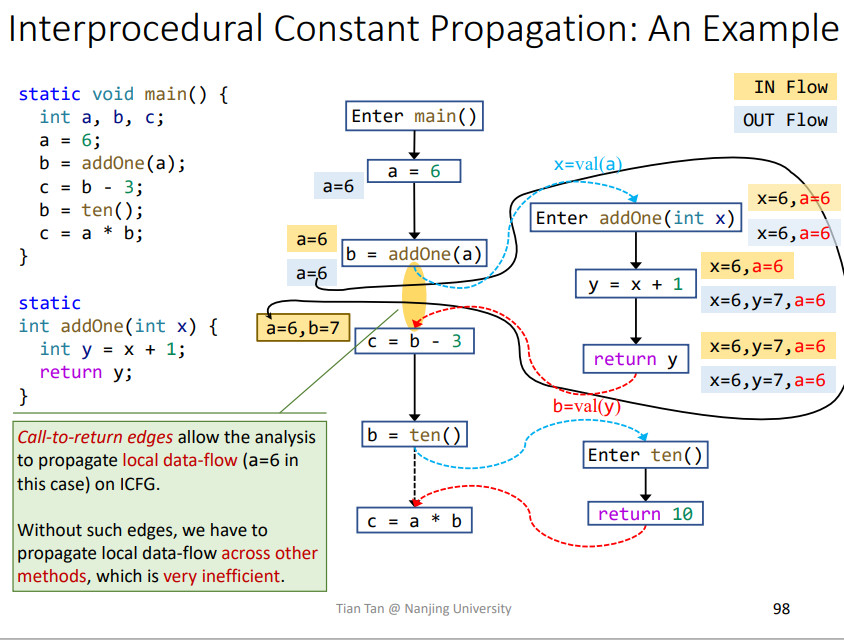
注意在传播过程的Node transfer时,需要kill掉返回覆盖的变量,比如这里就是b,这样在后面call-to-return edge和return edge进行join操作才会正确,如果不kill掉,就容易出现如下结果
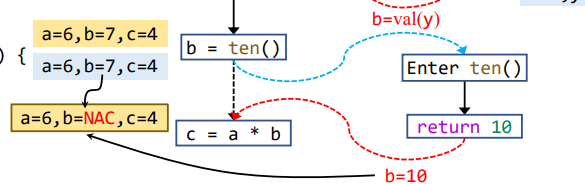
没有kill掉时,即从b=ten()这条call-to-return edge流下来的b为7,而从return edge流出来的b为10,依据之前常量传播的Control Flow
1 | IN[B] = ⊓p predecessor of B OUT[p] |
就会导致b的值为NAC,这是不准确的,其结果应该是被覆盖的那个值。
类比Intraprocedural Constant Propagation
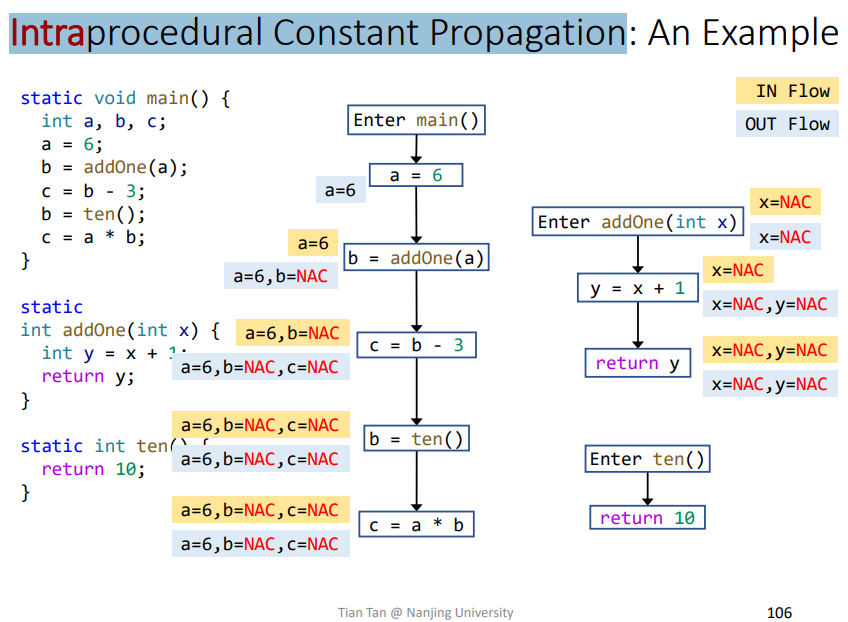
碰到函数调用就会产生NAC,不准确
总结

怎么通过类继承关系来创建调用图、过程间的控制流以及数据流分析的相关概念、过程间的常量分析
七、Pointer Analysis

1.Motivation
在常规的CHA方法中,由于一个方法调用可能指向多个方法,那么在遍历这些方法的时候,返回的值都有可能不同,然后再做join操作时,就有可能出问题。
比如如下的Constant Propagation

由于声明的类型为Number,调用get时有三个子类,那么就会有三个方法需要进行遍历,最后进行join时就会导致X=NAC。但是实际上,其实只会调用到One.get()方法,只会返回1,导致CHA不准确,那么就用到Pointer analysis,更加准确

2.Introduction to Pointer Analysis
指针分析是属于may-analysis,有很多年历史,包括现今指针分析还有很多问题没有被完善解决,所以还是有很多这方面的研究应用

例子
相关的一些表达方式如下,指针分析即一个程序作为输入,通过分析之后,得到一个指向关系表。

应用
应用很多,特别基础

3.Key Factors of Pointer Analysis
指针分析中主要的一些讨论点,问题以及相关的处理方法,这些处理方法都有各自的优缺点,主要关注于分析的准确度precision以及效率efficiency

Heap Abstraction
堆内存相信大家都很熟悉了,而在静态分析里面,由于堆是动态创建的,程序没有跑起来之前,不好确定程序究竟创建了多少个对象,而在有循环或者递归什么的时候,就更多了。

那么为了在静态分析中,确保分析过程能够停止下来,就不能在分析过程创建infinite个对象,就需要一种技术来对它进行抽象限制。
比较直观的一个例子就是把多个相同的对象都抽象成一个对象,如下所示
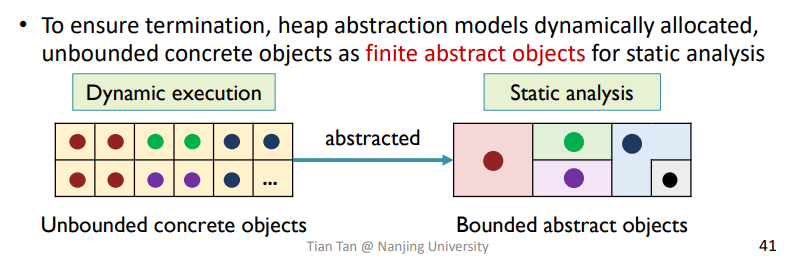
相关的抽象技术也是很复杂,很多
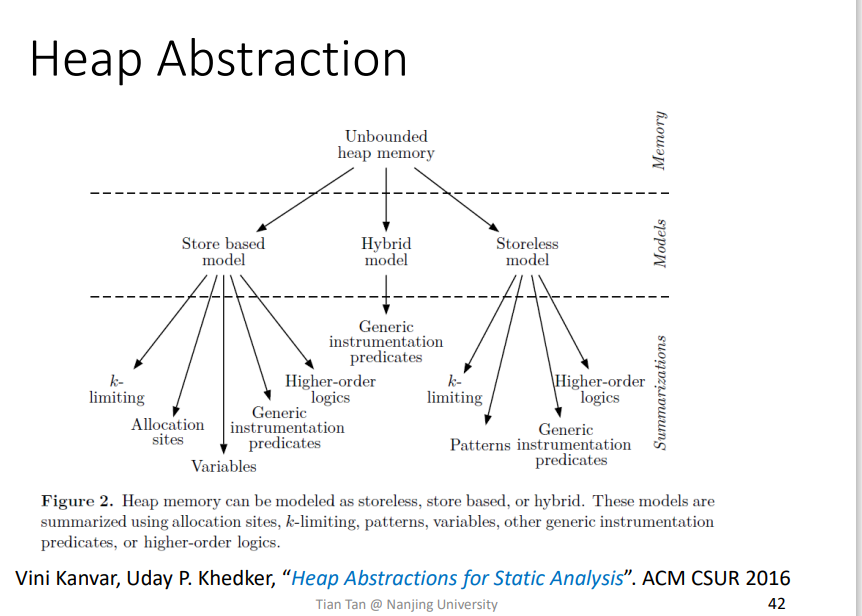
Allocation-Site Abstraction
这个就是Heap Abstraction中一种技术,Allocation-Site Abstraction创建的抽象技术

比如这里的O2是代表程序中第二行创建对象语句,实际上由于循环有三次,所以会创建三个对象,但是基于Alloction-Site Abstraction,可以将这三个对象都抽象成一个对象O2。
由于一个程序中对象创建点肯定是有限的,那么抽象对象也肯定会是有限的,能够terminate。
Context sentivity
一个方法被调用时依据传进来的参数不同,肯定也会对应不同的输出,所以针对同一个方法分析时,上下文敏感Context sentivity和上下文不敏感Context insensitive就是两种分析方法了,如下感觉图解很清楚。

会从Context Insentivity开始学习。对JAVA语言来说,Context sentivity提升是很明显的。
Flow Insentivity
之前学习的基本都是Flow Sentivity,即会依照程序的执行顺序,一步一步进行分析。但是Flow Insentivity则不会,它相当于将之揉杂在一起,不管程序的执行顺序。相关例子如下
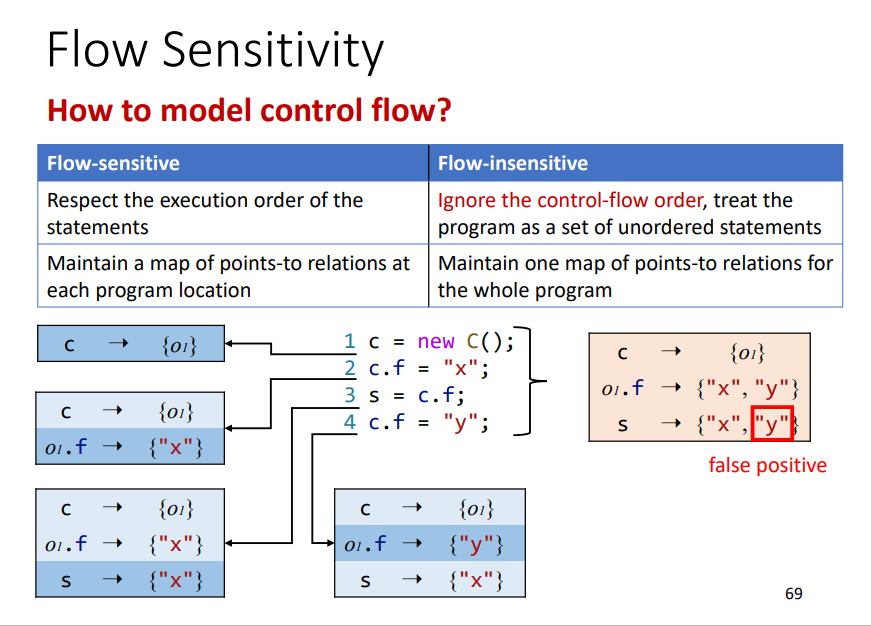
Flow Sentivity: 每一条语句的指向关系map都会随着该语句的执行做出相应的改变,开销比较大,每一点都需要进行维护,速度会慢很多。Flow Insentivity: 相当于把一个变量的所有可能的指向关系map都会全部列出来,不管语句的相关执行顺序,会导致一些精度的缺失。
对于Java而言,现今还没有相关的研究明显证明Flow sentivity比Flow Insentivity精度更好,所以现今大多都是针对JAVA的分析都是基于Flow Insentivity ,因为更简单更快。
但是对于C语言而言,Flow sentivity是会更好的。
Analysis Scope
分析的范围,通常是两种,即Whole-Program全程序和Demand-driven需求驱动

Whole-Program: 即整个程序所有变量的指向关系都会分析出来。更加简单全面,比较主流。Demand-driven: 即需要哪一部分就分析哪一部分,这里就好比需要分析z.bar(),那就只需要z的指向关系了。相比Whole-Program,有时候其效率其实也差不多,所以大多选择Whole-Program。
4.Pointers in Java
关注的指针类型

基本只关注其中两种指针,即local variable,这个其实和Static field差不多。
另一个就是Instance field即类中的成员属性指针,这个和Array element基本归为一类,但是在处理的时候需要对Array element一些抽象,不关注其中的索引,而只关注其保存的指针,如下

将索引抽象成一个,因为在实际的程序中,索引很难判断出来,尤其在循环中,索引大多都是一些变量什么的,所以不好进行判断,那么就抽象成一个就好了。
关注的指针语句

有两个需要特殊说明一下
Store: 有时候可能会有很复杂的语句,比如x.f.g.h = y,但是将之转换为三地址码,就比较简便了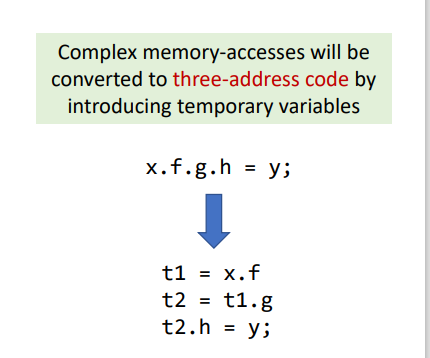
Call:JAVA中存在三种类型的Call,但是我们关注于处理Vitural call的情况,这个比较复杂,这个会处理其他也会处理了。
总结

理解指针分析,影响指针分析的几种要素,以及在分析过程中需要处理分析的对象。
八、Pointer Analysis Foundations (I)

相关概念定义

pt就相当于一个map,key->value。pt(p)即变量p指向的对象的集合,比如x = new T(),则pt(x)就代表x指向的对象集合,因为我们用的是Flow Insentivity这个技术,所以是pt(x)是一个集合。
1.Rules

即横线上面的为前提条件premises,当前提条件满足,则可以推导出结论conclusion。
Rule : New
无条件得到

Rule : Assign
比如一条语句为x=y,如果premises满足O𝑖 ∈ pt(y),那么即可推导出conclusion为O𝑖 ∈ pt(x),如下

即将pt(y)集合中的对象Oi加入到pt(x)这个集合中
Rule : Store
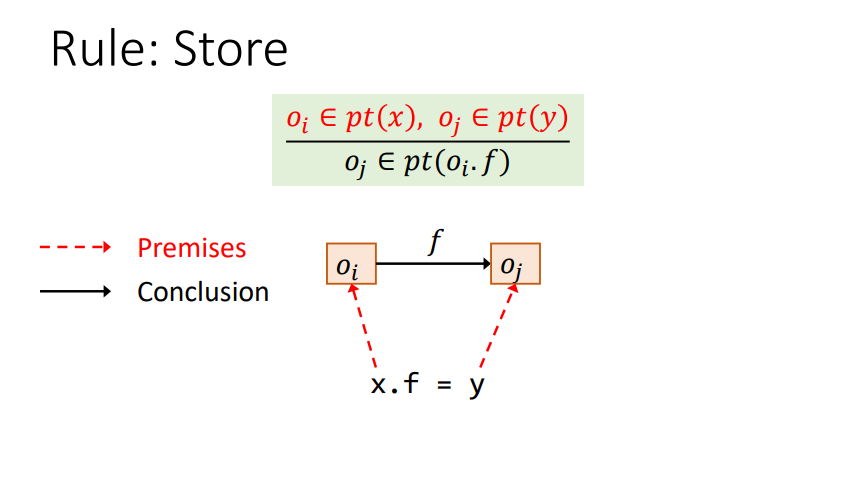
需要理解一个pt(Oi*f)的含义,即某个对象成员指向的对象的合集。
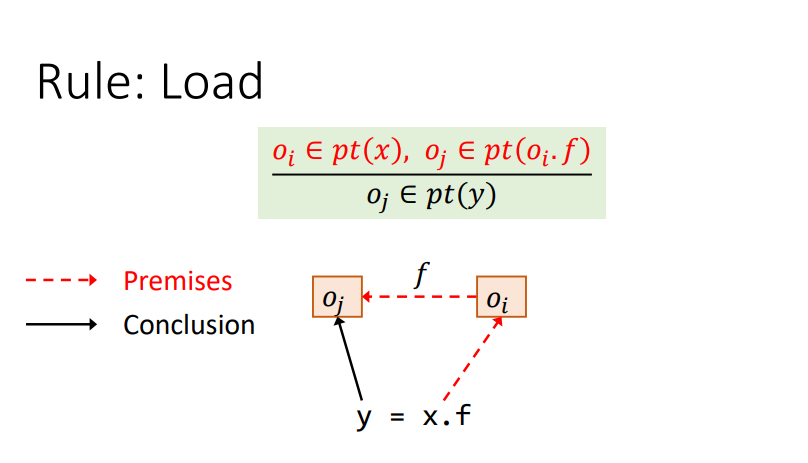
Rule : Load
和前面差不多
总结
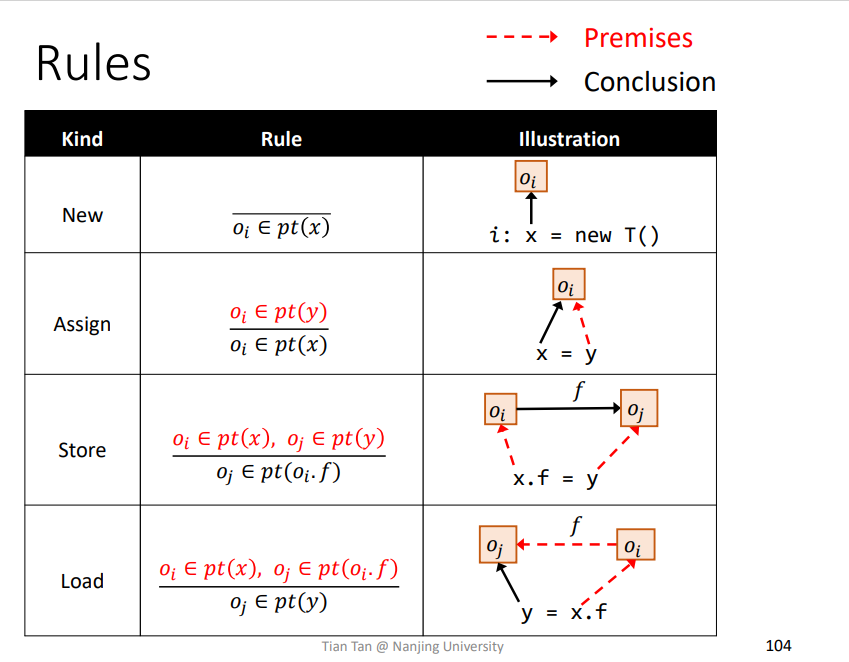
其实就是形式化表达了这些语句,方便后续推导
2.How to Implement Pointer Analysis
指针分析关键点就是如果在一个指针发生变化时,如何将变化传递给和该指针有关的其他指针。
使用图来传播指针,传输给该指针的后继。

Pointer Flow Graph(PFG)
概念
NodesPointer = V ⋃ (O × F),即节点n表示一个指针变量,或者说一个抽象对象的一个field。EdgesPointer × Pointer,某条边x->y,代表x指向的对象pt(x)也**可能may**会流向y指向的对象pt(y)。
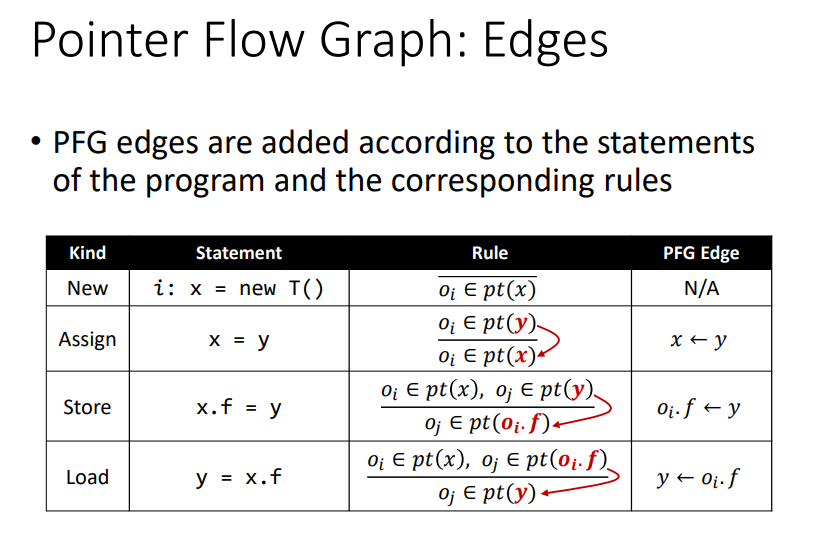
节点n即相关的变量,边edge即流向关系。
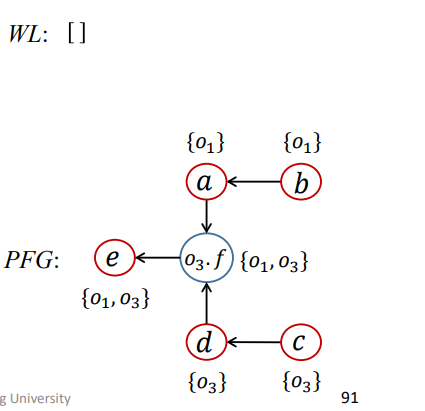
实例
如下图所示,感觉还是挺清楚的

需要注意的是,c.f需要表示成Oi.f才行,才是一个真正的指针。
那么指针分析就变成在指针图PFG上分析指针集传播过程的问题了。

Propagate points-to information on PFG
在上述建图的过程中,其实也涉及到指针传播的相关信息,并不是说在建立PFG时不考虑传播信息。比如说在构建c.f=a时,我们需要先知道的是c的指针流向,即Oi。传播和构建是相辅相成的,动态构建的。
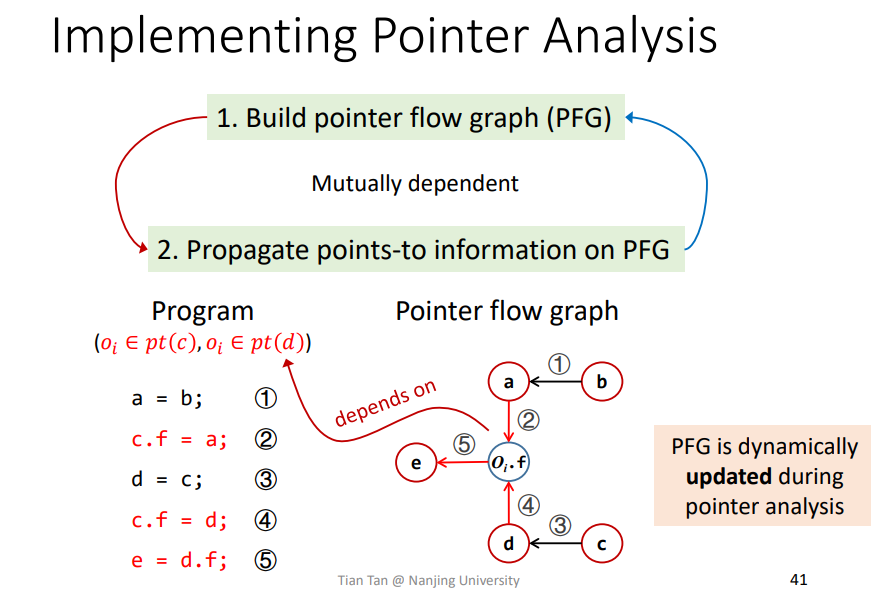
3.Pointer Analysis: Algorithms

其中S即为输入程序语句的合集,PFG就是指针流向图,比较需要关注的就是WL以及其中的数据含义
Worklist存储需要被处理的
pair,其中每个pair形式大概为<n,pts>,代表说pts这个对象集合需要被传播到指针n指向的对象集合pt(n)中。比如一个
Worklist为[<x,{Oi}>,<y,{Oj,Ok}>,<Oj.f,{Ol}...>,表示{Oi}需要传播到pt(x){Oj,Ok}需要传播到pt(y){Ol}需要传播到pt(Oj.f)- …..
Handling of New and Assign
算法的前部分是用来处理New和Assign的
Initialize
首先进行相关的初始化
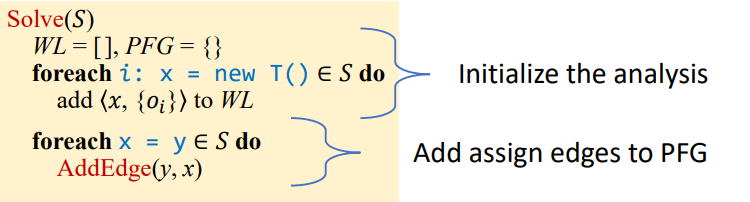
遍历所有New和Assign语句
New语句即将相关pair添加到WL中Assign即需要在PFG中添加相关传播关系的边edge
- 如果
s->t这条边在edge中存在则说明有边了,不需要添加了,否则就添加到PFG中 - 添加完成之后,还需要判断
pt(s)是不是空的,如果不是空的则需要将对应pt(s)传播到t指向的对象集中,所以需要将它加入到WL进行后续分析工作
- 如果
Propagate
在初始化之后,就需要遍历WL进行传播了
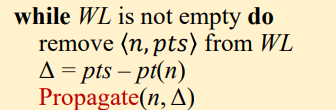
首先从
WL中取出在
pts中找到pt(n)中不存在的对象集Δ,因为在pts中存在的对象,在pt(n)中也可能存在,所以需要去掉之后再进行合并操作,避免重复。相关例子如下
注:最开始其实所有指针的对象集
pt(x)都是空的,那么为什么需要去重呢,这个后面会讲到。应该是在动态的创建PFG过程中,pt(x)会不断更新,也会重复被计算。如果不去重的话,其后继中已经被传播的部分就可能再次被传播,从而做了无用功,影响效率。然后就是传播
Propagate(n,Δ)
- 如果
pts不为空,就并入到pt(n)中,这个就是实际的传播过去了。 - 但是传播到
pt(n)不够,还需要传播到n可以流向的其他所有节点。所以需要遍历PFG中所有的n->s,将<s,pts>加入到WL中等待后续处理
- 如果
Differential Propagation
这里就是解释了为什么需要差异传播Differential Propagation去重,即避免已经被传播过的信息再被传播造成无用功。
比如如下情况
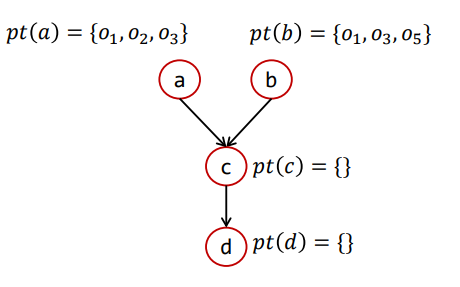
假设a先传播,结果如下
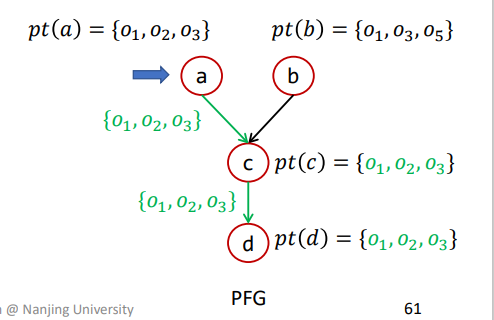
那么b再进行传播,此时c就相当于n,那么pts={O1,O3,O5},pt(n)={O1,O2,O3},如果不进行差异传播则过程如下
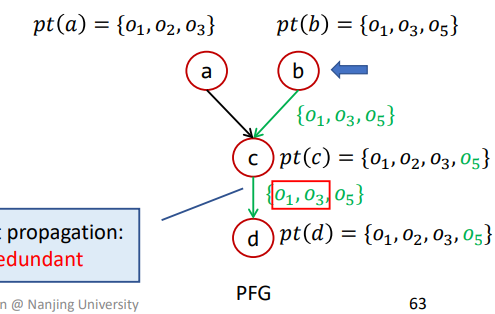
导致{O1,O3}被重复传播
如果进行差异传播则过程如下
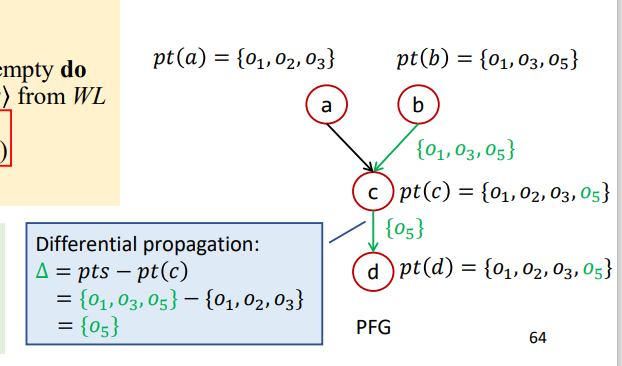
这样已经被传播过的就不会再被进行计算传播了。
不过这里有个前提,即该算法在每次传播的时候已经确保了pt(n)已经被传播给了n的所有后继。
Handling of Store and Load
算法循环的后半部分是用来处理Store和Load的

关于x指向对象相关成员的所有Store和Load语句都会进行处理,需要遍历所有需要传播的对象集合,即Δ
这里需要注意的是,再添加边时,不一定能够添加上。因为在处理x.f=y时,之前可能已经有了A=x;A.f=y这样的,导致在PFG中其实有了这样一条边,就不用再添加了。这也是在AddEdge中进行是否存在边判断的原因。
实例

首先初始化WL=[]、PFG={}
New处理
首先是New处理
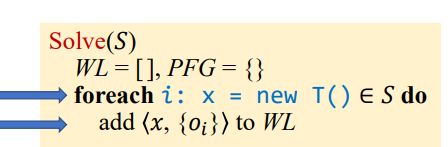
语句1和3有New操作,对应O1和O3,添加到WL中
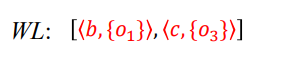
Assign处理
然后是Assign处理

语句2和5有Assign操作,进行AddEdge操作

使得PFG结果如下
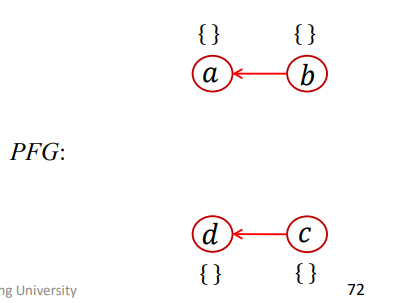
由于还没进行传播操作,所以这里b对应的pt(b)和c对应的pt(c)还是空的。
那么在以上两种初始化操作完成后,结果如下
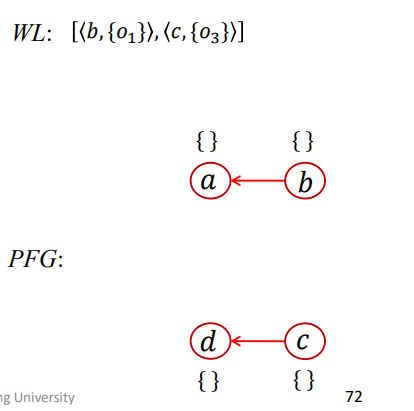
WL处理
Load和Store是在这一部分进行迭代的
第一次迭代
1 | WL = [<b,{O1}>,<c,{O3}>]; |
结果如下
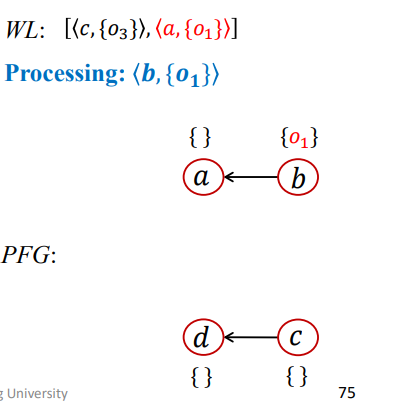
第二次迭代
1 | WL = [<c,{03}>,<a,{O1}>]; |
结果如下
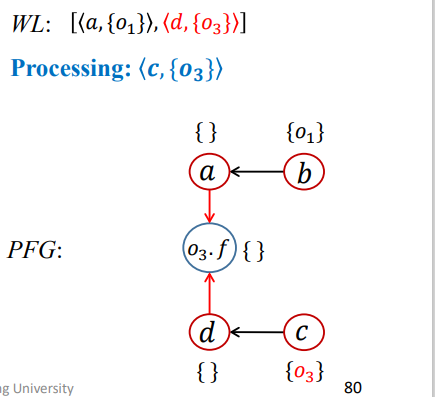
第三次迭代
1 | WL = [<a,{O1}>,<d,{O3}>]; |
结果如下

第四次迭代
1 | WL = [<d,{O3}>,<O3.f,{O1}>]; |
结果如下
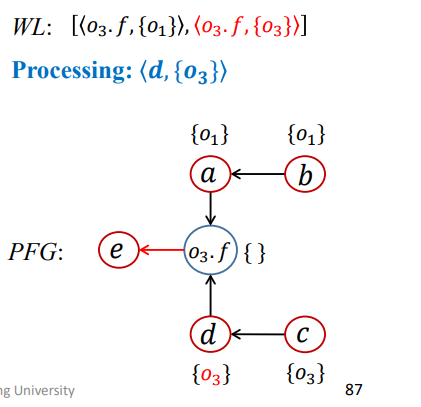
第五次迭代
1 | WL = [<O3.f,{O1}>,<O3.f,{O3}>]; |
结果如下
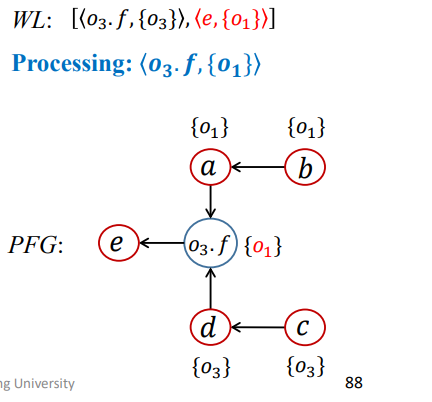
第六次迭代
1 | WL = [<O3.f,{O3}>,<e,{O1}>]; |
结果如下
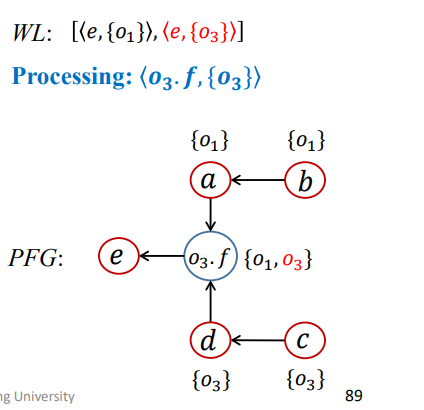
第七次迭代
1 | WL = [<e,{O1}>,<e,{O3}>]; |
第八次迭代
和第七次类似
1 | WL = [<e,{O3}>]; |
WL为空,算法结束,最终结果为
总结

理解指针分析的规则,PFG,以及对应的算法
九、Pointer Analysis Foundations (II)
4.Pointer Analysis with Method Calls
结合之前的CHA和指针分析,来做过程间的指针分析

在指针分析的过程中做call graph,即on-the-fly call graph construction。
指针分析更加准确,在做过程间的分析时就会使得call graph做的更好,因为不用再依据声明的对象来寻找方法,而是直接通过指针指向的对象来获取方法,更加准确。
而call graph做的越好,其虚假边就会更少,从而指针分析就会更加准确。这两者是互相成就。
只会分析可达方法,不可达方法不进行指针分析,提升精度和效率。
Rule : Call

符号含义:
Dispatch(Oi,k): 和之前一样,通过传入对象指针和函数签名寻找函数,本类找不到找父类M_this: 函数m中的this变量M_pj: 函数m中的第j个参数M_ret: 函数M的返回值
即相关的传递指针
$$
\begin{align}
&O_i\in pt(x),m=Dispatch(O_i,k)\ &=>&\ O_i\in pt(m_{this})&(传递this指针,不用在PFG连边)\
&O_u\in pt(a_j),1\leqslant j\leqslant n\ &=>&\ O_u\in pt(m_{pj}),1\leqslant j\leqslant n&(传递参数指针,需要在PFG连边)\
&O_v\in pt(m_{ret}) &=>&\ O_v\in pt(r)&(传递ret指针,需要在PFG连边)\
\end{align}
$$
需要注意的是this传递的时候是不用在PFG中进行连边处理的,因为如果连边处理的话,那么pt(x)包含的所有对象都会流入到不同的类中,情形如下,就会多出无效的对象要处理,浪费资源。

Algorithms
相关算法

相关概念已经解释很清楚了
AddReachable(𝑚)
程序最开始、以及新的call graph边被添加时都会调用到,该方法的功能其实就是对于一个方法中所有可达语句进行相关的初始化。
可以看到最开始进入的方法是m^entry,借助是否发现新方法来对WL以及PFG进行更新。
对于最开始调用,即m^entry作为新方法传入时。和之前差不多,只是添加了一些关于是否可达的语句进来,用来进行New和Assign相关对象指针初始化、WL和RM的初始化、以及PFG的初始化。
而对于后续发现新方法,都是进行针对新方法的一些指针分析初始化,类似的。

注:新方法的初始化是不能对Load和Store以及Call进行处理的,因为这些都需要依赖于New和Assign。
ProcessCall(𝑥, O𝑖)
上述初始化之后的后续部分都差不多,只是在大循环中多了一个ProcessCall进行新方法的发现添加。

针对某个变量的WL的处理,都需要对所有可reachable的函数进行处理传递
Output
得到相关的指针集(Points-to Relations (pt))以及调用图(Call Graph)
实例

初始化
首先是初始化,经过AddReachable(m_entry)

得到如下结果
1 | RM = {A.main()} |
WL处理
第一次迭代
1 | Processing = <a,{O3}>; |
结果如下

第二次迭代
1 | Processing = <b,{O4}>; |
最终结果如下:

第三次迭代
1 | Processing = <B.foo/this,{O4}>; |
最终结果如下

第四次迭代
1 | Processing = <r,{O11}>; |
结果如下:

第五次迭代
1 | Processing = <y,O3>; |
结果如下:

第六次迭代
1 | Processing = <c,O11>; |
结果如下

至此整个算法结束,得到最终结果CG和PFG

总结

理解对于方法调用的指针分析规则,理解过程间的指针分析算法,以及两者相互依赖的情况。
十、Pointer Analysis Context Sensitivity (I)
Problem of Context-Insensitive Pointer Analysis
1 | void main() { |
Context-Insensitive:如果利用之前学到的指针分析进行分析的话,就会导致对于id函数的返回值n,其会包含两个对象,即{O1,O2}。从而导致n->x,y的流向中,会将{O1,O2}传递给x,y,导致x,y也包含两个对象,如下所示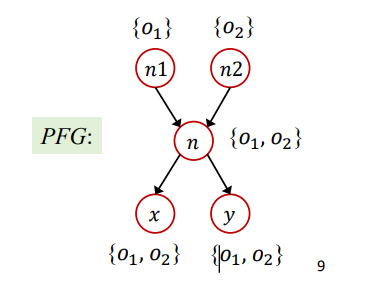
那么在后续的调用中,
int i = x.get();这代码进行常量传播分析时,就会导致i = NAC,这是错误的结果,不准确。Context sensitivity:利用上下文敏感进行分析的话,将每一次的函数调用分为不同的情况进行分析,这样就可以得到如下精确的PFG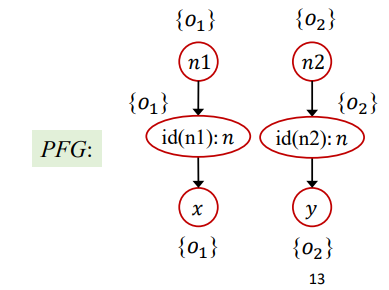
这样进行常量传播分析时就能得到精确的结果了。
1.Introduction
Imprecision of Context Insensitivity (C.I.)

依据之前的例子也可以看出来,一个函数每一次调用时,其上下文,数据流等可能会不同,那么其结果也可能会不同。而不敏感的分析中,这些所有的结果都会混合到一起,即混合到该函数的返回变量中,这样就会导致混合的数据流传播时污染了其他的数据流,导致虚假的一些信息。
Context Sensitivity (C.S.)
call-site sensitivity (call-string)

比较古老以及好理解的一种方法,即某点调用时,它的上下文即为Call Site。比如如下的代码

对于id方法而言有两个上下文:[1]和[2],进行调用时就会作克隆标记,方法为Cloning-Based进行分析

Context-Sensitive Heap

用以提高精度,将创建的对象依据上下文进行更加细粒的区分
1 | void main(){ |
比如上述代码中,如果使用C.I.进行分析,那么无论什么时候调用函数newX,最后都只会得到一个对象O_10。但是如果在C.S.中使用该方法进行细粒化,就可以在不同的调用点对O_10进行区分,比如这里就可以将O_10分为C3:O_10和C6:O_10,类似如下
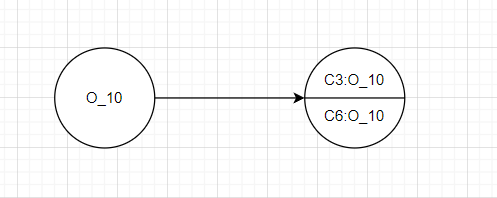
这样就精度更高,避免数据流的混合。
实际例子

其实通过上述图片可以大概推导出来,在C.S.heap的技术中,主要是针对传入的上下文做一个标记,标记出不同上下文下得到的对象,这样就可以更加精确。
C.S.heap要和C.S.共同使用才能发挥作用,C.S.heap和C.I.是不能发挥作用的,如下例子所示。

2.Context Sensitive Pointer Analysis: Rules
Domain

主要加入了一个修饰符c,表示上下文
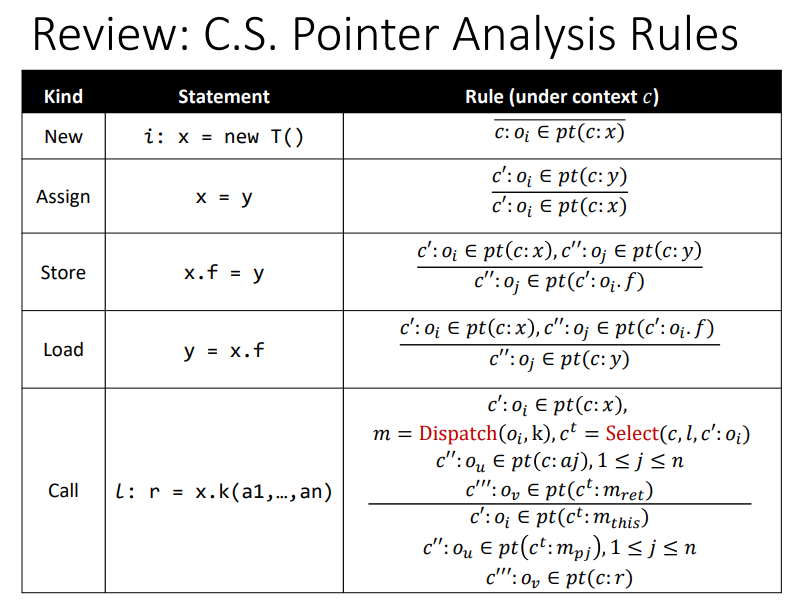
Rules

类似之前的一些规则表格
Rule: New

这个就很容易理解了
Rule: Assign
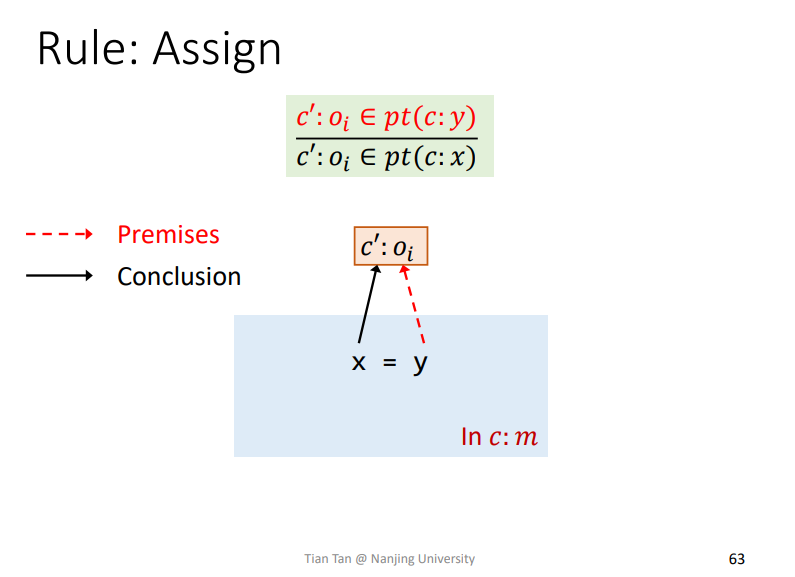
这个也容易理解
Rule: Store
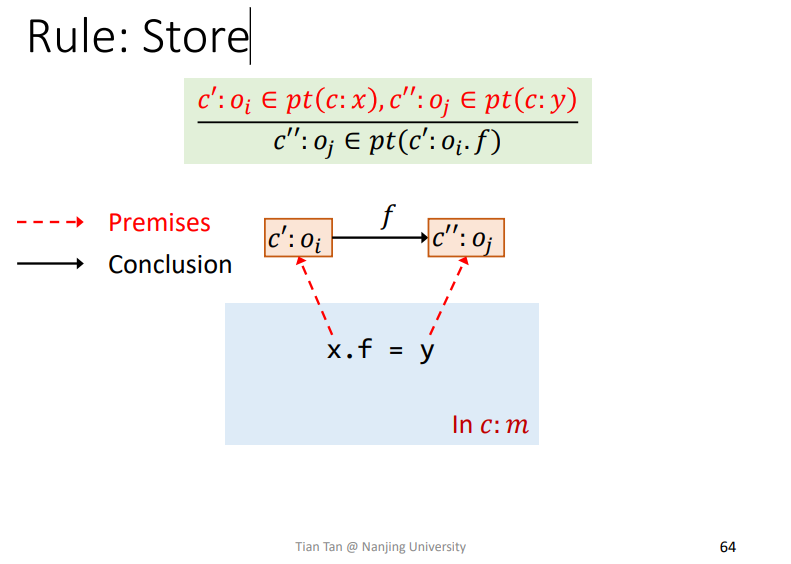
容易理解,就是理清楚各个变量指向对象的上下文C在哪里
Rule: Load
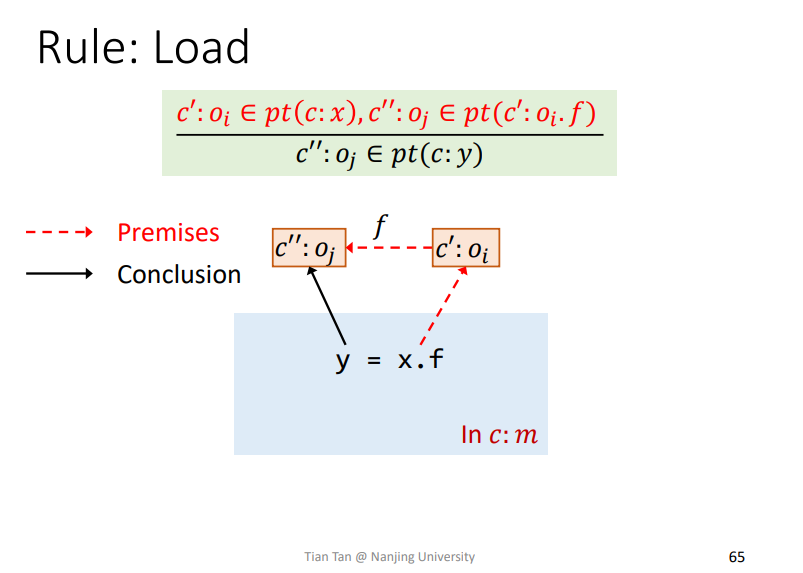
类似的
小总结
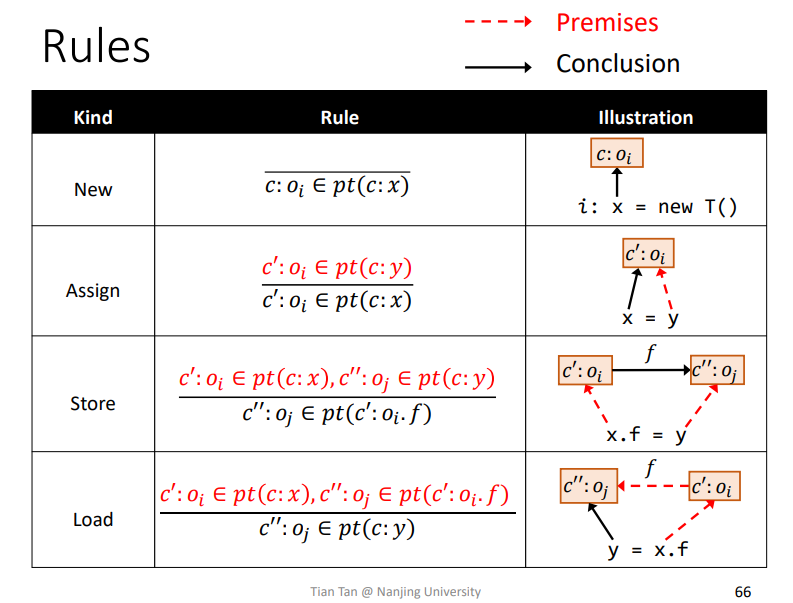
Rule: Call

当进行方法调用时,Dispatch求解函数,然后Select得到上下文之后,就可以对应进行相关变量的值,或者指针对象传递了。和之前也差不多,就是加入了相关的上下文。
总结

理解context sensitivity (C.S.)以及context-sensitive heap (C.S. heap)的相关概念,以及这些方法为什么能够提升精度。关键点就是经过相同的代码,但是其上下文可能不同,如果混合了数据流就会比较虚假,所以需要进行精确区分上下文。
C.S.指针分析的规则。
十一、Pointer Analysis Context Sensitivity (II)
一些小的回顾就不说了
3.Context Sensitive Pointer Analysis: Algorithms
主体框架、流程和原来的差不多,加入上下文敏感了。

首先是一些概念,和之前类似,加入了上下文

具体例子如下
RM即
reachable methods可达方法集合中所有方法都会有上下文,下面的就代表在Ct上下文下可达的方法。
CG即
call graph调用图中,如下c代表在调用时的上下文
$$
c:2\ \ \ \ \ \ c^t:T.foo(A,A)∈CG
$$
AddReachable(𝑐:𝑚)
最开始进入的入口函数为[]:m_entry,此时没有什么上下文,所以就为[],其他的和之前类似,加入上下文

AddEdge/Propagate
和原先的一样,不需要怎么管

因为Propaget传播依据现有的PFG进行传播,不需要管上下文。而AddEdge连边也是一样的,只是在PFG中连上两条边,并且指导后续的WL工作进度,不需要上下文。
Load/Store
主要看主体部分的Load/Store部分

需要注意到图中用红色框起来的部分,每一个c:x和对应的c:y的上下文是一样的,这个应该也不难理解,因为传递的是指针对象集合,其包含的上下文也应该是一样的,不然可能不同的上下文导致不同的对象,其field也会可能发生改变。
ProcessCall(𝑐:𝑥, 𝑐′:O𝑖)

加入相关上下文,以及一个Select(c,l,c':Oi)这样一个用来选择上下文的函数,该函数依据自己的算法设计,进行上下文的选择,比如选中多个lable等,用来唯一标识,这个后面会详细讲一下。
注:该算法大多不涉及循环处理,因为开销比较大。其他领域有这个方面的。
4.Context Sensitivity Variants
主要讲Select
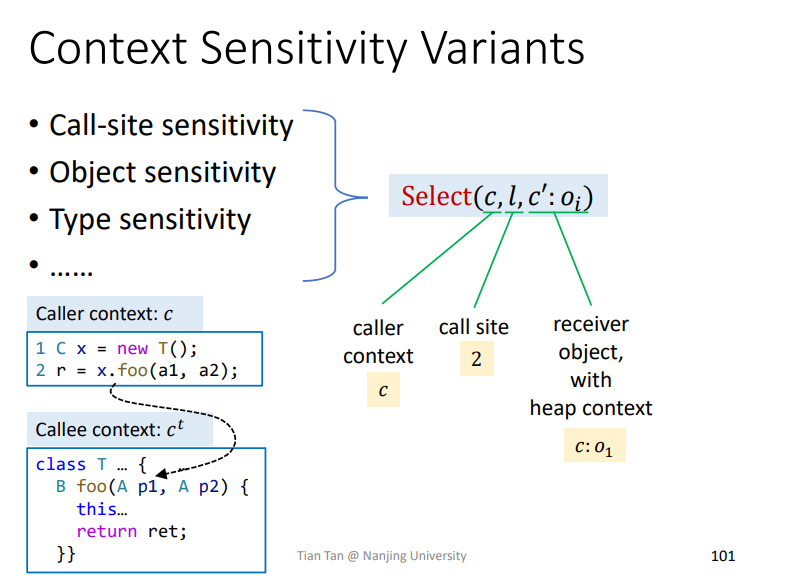
如上所示,各种上下文都可能会被考虑到。
Context Insensitivity
其实对于C.I.这个技术而言,其本质就可以当作是Select选择出来的上下文为空,即

Call-Site Sensitivity
Olin Shivers, 1991. “Control-Flow Analysis of Higher-Order Languages”. Ph.D. Dissertation. Carnegie Mellon University.论文提出,方法叫做Call-Site Sensitivity ,或者call-string Sensitivity,或者k-CFA(Control-Flow Analysis)
其实就是一个call chain调用链,
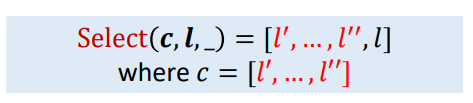
即当进行ProcessCall的Select时,做的工作就是一个并集,将当前的调用点加入到之前的上下文中,形成当前新的上下文,调试程序的时候就经常可以看到,提供的例子如下

但是这种有递归的情况中,由于每次碰到新的上下文方法,都会进行分析,所以就会导致分析出无穷无尽的调用链和对应的调用方法,那么就需要引入一个能够进行终止的方法k-Call-Site Sensitivity/k-CFA。
k-Call-Site Sensitivity/k-CFA
加入一个k个数的限制

即确保上下文个数为k个,如果超过了,就舍弃掉最老的上下文。
比如k=2,在[2,3]上下文中需要加入[4],那么分析发现上下文个数超过k个,那么就舍弃掉2,新的上下文变成[3,4]。相当于是个缓存了。
实例
相关例子如下
1 | interface Number { |
省略掉C.S.Heap方法以及m函数里的this变量。
初始化
首先是初始化,经过AddReachable

得到结果如下
1 | RM = {[]:C.main()} |
WL处理
第一次迭代
1 | Processing = <[]:c,{O3}>; |
第二次迭代
开始情况如下
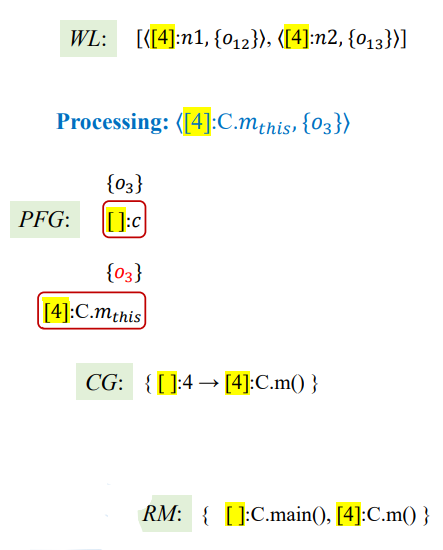
1 | Processing = <[4]:C.m_this,{O3}>; |
结果如下:
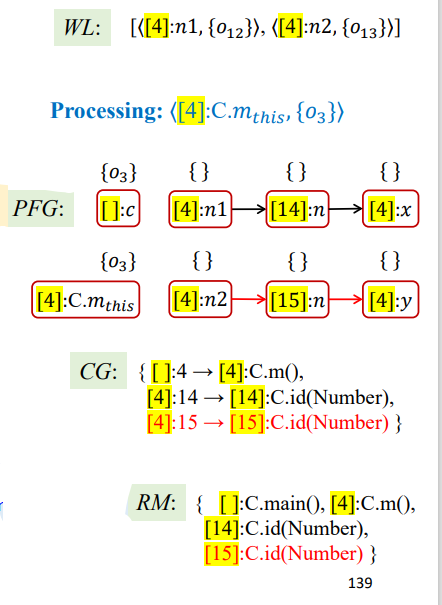
后面几次迭代就是一些传播了,大致概括如下
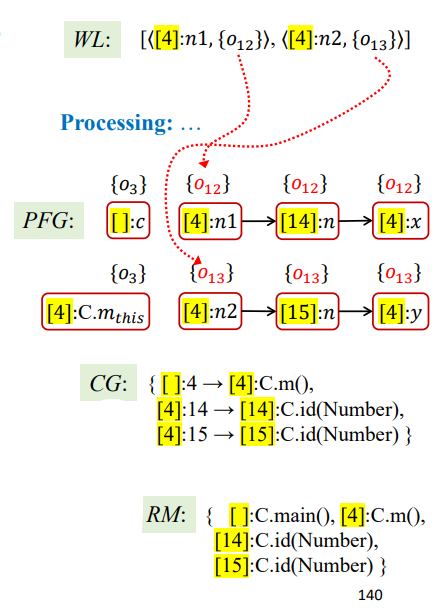
第三次迭代
1 | Processing = <[4]:n1,{O12}>; |
第四次迭代
1 | Processing = <[4]:n2,{O13}>; |
第五次迭代
1 | Processing = <[14]:n,{O12}>; |
第六次迭代
1 | Processing = <[15]:n,{O13}>; |
第七次迭代
1 | Processing = <[4]:x,{O12}>; |
第八次迭代
1 | Processing = <[4]:y,{O13}>; |
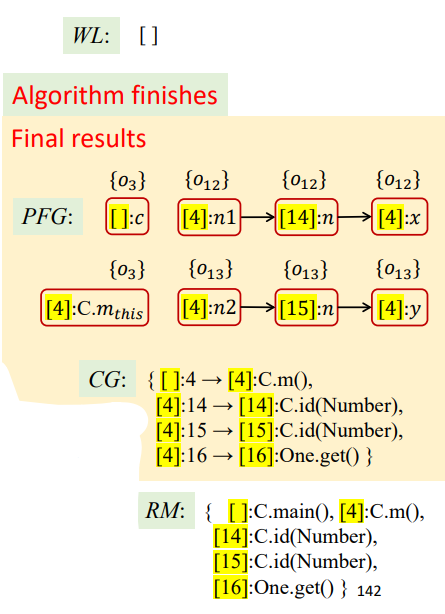
到此WL清空,算法结束,最终结果如下
Object Sensitivity
和之前提到的K-Call-Site方法类似,以对象作为上下文的参照

实例

即针对调用时的this对象来作为一个上下文的标识。
Call-Site和Object-Sensitivity对比
这里把1-Call-Site和``1-Object-Sensitivity`进行一个对比,结果如下

在该例子中,1-Object更加准确,但是另一个例子如下

1-Call-Site会更加准确。
所以在理论上,两者没有办法进行比较,但是在实际操作中,针对OO语言来说,Object Sensitivity更加好一点。

这个相关的一些对比如下,是两位讲课老师发表的论文,该论文提到一种更加行之有效的方法,只针对程序中一小部分内容运用Object-Sensitivity方法,会更加有效,不过这部分内容也需要一定的资源进行计算。
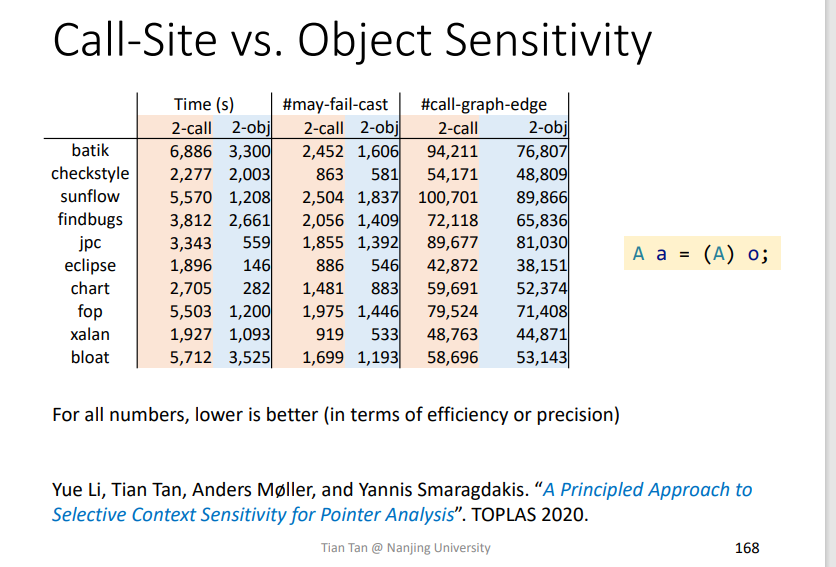
从运行的时间(越短越好),调用图的边数(越少越好),以及cast的转化失败可能性(越低越好)来对比,object-Sensitivity在OO语言上表现更好。
Type Sensitivity
也有很多其他上下文挑选条件,比如Type Sensitivity

即在调用点所在类的类型作为筛选条件。
该方法的精度小于等于Object-Sensitivity,但是速度更快。而在实际上Type-Sensitivity的精度与Object-Sensitivity相差不是很多
总结对比
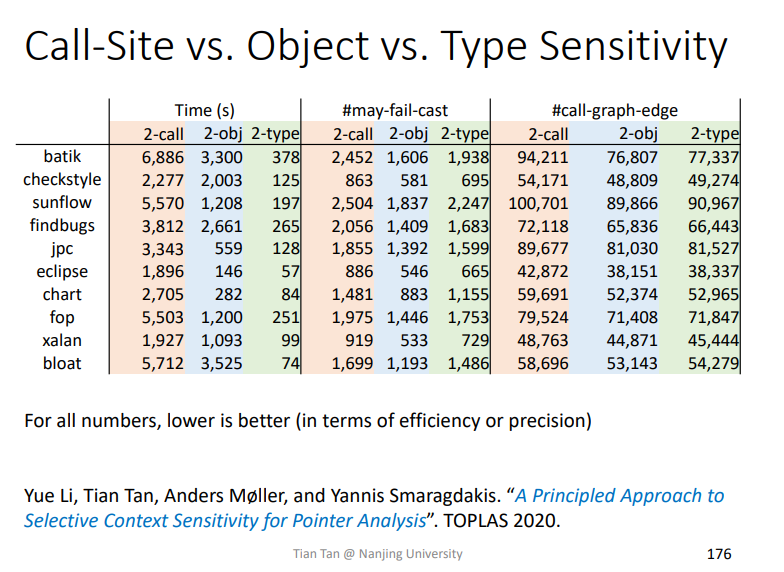
以上三种方法针对OO语言,最终对比如下

总结

理解上下文指针分析的算法,通常的上下文几个variants变种,以及不同variants变种之间的对比差异等等。
十二、Static Program Analysis
1.Information Flow Security

即定义程序中变量的安全等级,明确不同安全等级之间的流动策略,以及相关的访问权限策略等。
Information Flow
Information Flow信息流相关概念就不用太说明了
Security levels(Classes)

比较常见的就是two-level policy,低等密级和高等密级,或者一些更加复杂的

Information Flow Policy

常见的策略就是Noninterference policy非干涉策略,即高密级的不能流向低密级的,低密级可以流向高密级的
Noninterference

由上述例子大概可以知道该策略的相关的信息流动规则。
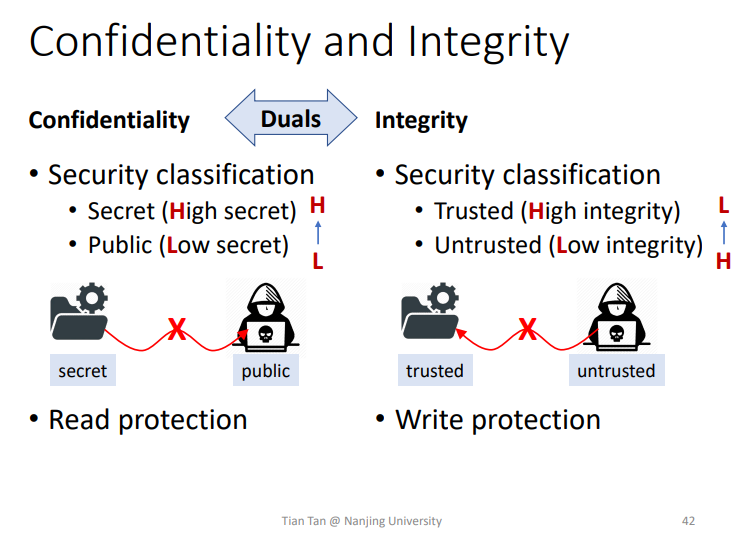
2.Confidentiality and Integrity
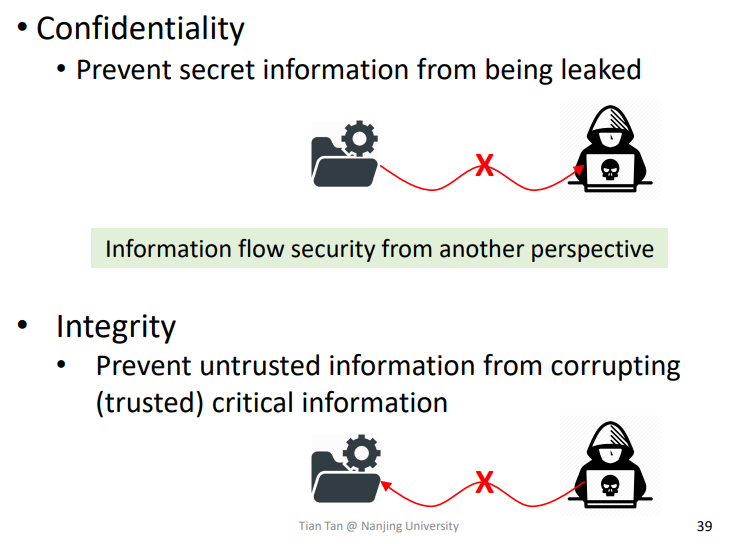
两者所防御的点不一样,一个像Confidentiality读保护,一个像Integrity写保护
Integrity
保护数据的完整性

即防止不可信的数据影响到本地的相关数据程序。
此外还有更加广泛的定义

即数据的Completeness完整性、Correctness准确性、Consistency一致性都是在Integrity的定义下。
Confidentialityt
保护数据的保密性,即数据不被泄露。
3.Explicit Flows and Covert Channels
Implicit Flows

可以通过判断public_L的值,判断出secret_H的信息,即Implicit Flows隐式流。
更多例子

上述的各个语句,都可以通过特定的情形判断出secret_H的相关信息
Covert/Hidden Channels

channels: 通过计算来传递信息的机制称为Channels信道Covert Channels: 一个主要目的不是信息传递的信道,但是该信道仍然将信息传递出来了,那么这个信道被称为Covert Channels隐藏信道
以上提到的一些信道其实都是这里定义的Covert Channels,都会传递出一定的信息,有点像一些侧信道攻击。
Explicit Flows
那么相对于Implicit Flows隐藏信道的就是Explicit Flows显式信道,会传递出更多的信息,如下例子所示。

4.Taint Analysis
针对关心的数据打上标记称为Tainted data,那么依据该数据的源头Source进行分析,尝试寻找tained data是否会流到某个敏感点sink,比如常见的system函数。

课程中老师讲到如下的一些例子,类似的。

Taint and Pointer Analysis
可以将指针分析和污点分析相结合,Tainted data污点数据作为一个指针对象,sources作为allocation sites,然后用指针分析来传播tainted data。

Domains and Notations

加入了一个污点数据定义,包含在之前的对象集合中

感兴趣的创建对象点为Sources,敏感方法为Sinks,最终可以输出一个pair,<i,j,k>表示从source_i的污点数据可能会流到k个参数的call_site_j这个sink方法中。
Rules
Rules:Sources
处理Sources的方法

即在指针分析的call时,某个调用点会调用到属于Sources的方法m,那么就会创建一个t_l污点数据放入该方法返回值的指针集pt(r)里面。
Rules:Propagate
传播的过程和指针分析类似,因为污点数据其实就是一个对象集合。
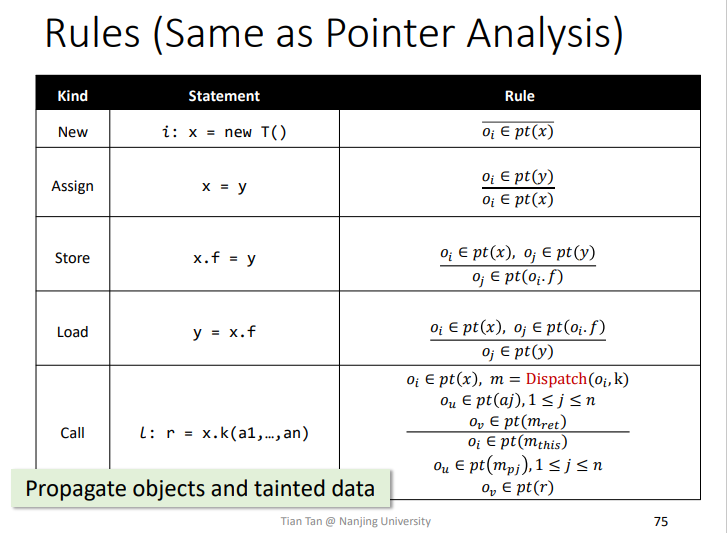
Rules:sink

当某个点调用到属于Sinks的方法时,如果方法调用参数中包含污点数据,那么就会将一个pair<j,l,i>加入到TaintFlows中方便后面进行输出。
实例

首先是污点分析的tainted data的创建,这里就是t3加入到pt(pw),然后就会随着pt(pw)一直流动到s中,直到调用到sink点时,检测到传入的参数中包含pt(pw)这个tainted data,就可以加入到TaintFlows了。
其中<3,7,0>代表在3处的tainted data会流向到7处的sink,参数位置为第0个参数。
总结

信息流安全的概念,信息的完整性和保密性,显式和隐式的信道,以及污点分析的相关使用。
十三、Datalog-Based Program Analysis
基于Datalog来进行程序分析
1.Motivation

Imperative命令式语言告诉计算机怎么做,类似
C语言Declarative声明式语言告诉计算机要做什么,类似
SQL语言
Pointer Analysis, Imperative Implementation
worklist:Array/list?- 先进先出吗?
points-to set(pt):Hash/vector?
PFG nodes:- 变量和节点的关联
variables and relevant statements变量和相关语句的关联
Pointer Analysis, Declarative Implementation (via Datalog)
通过Datalog来实现指针分析比较好实现

2.Introduction to Datalog
Datalog = Data + Logic
最开始是从数据查询语言发展而来

Predicates(Data)

这张表中,Predicates谓词即为Age,某个Statements在表中即为fact,不在就不是fact。
Atoms

Atoms在Datalog语言中是最小的语句,形式如同Age("Xiaoming",18)
relational atom
形如P(X1,X2,…,Xn)被称为关系型Atoms,比如Age(“Xiaoming”,18),代表一种关系。
Rules

感觉就是通过数据Facts,然后给定规则Rules,最后得到一个结果Datalog program
EDB and IDB Predicates

这里不是很懂这两个数据库的概念,后面再来看看把,其中EDB是不能修改的。
Logical Or

逻辑or的操作符为;,运算优先级小于逻辑and。
Negation

逻辑非的运算符!,类似的。
Recursion
递归的性质

即某个IDB某些数据加上一些东西也可以推导出该IDB的某些数据,就有一个递归在里面。
正是有了递归使得Datalog变得更加丰富,不再像只是简单查询的类似SQL的语言。
Rule Safety
在Datalog中的rule存在safe的概念

比如上述图片提到的例子,x>y中的x是无穷的,!C(x,y)的元素也是无穷的,这样的就是unsafe的。
一个safe Rule中的所有变量都只能出现在non-negated,即不是否定!的关系Atom中。
在Datalog中只有safe rule可被允许。
Recursion and Negation

这种没有意义的规则是不能写的,没有含义,Datalog也不会允许。
Execution of Datalog Programs

不同的语言引擎其规则大同小异
Datalog具有单调性,其Facts只会单调递增,并且Datalog程序一定会终止,因为其Monotonicity单调性以及safe rulety。
3.Pointer Analysis via Datalog
相关概念
EDB

EDB:能直接从程序中得到的关系数据库,比如New、Assign等等IDB:最终的指针分析结果Rules:指针分析设定的规则
比如如下的情况

Rules

基本都是一一对应的,对应理解就好
Call
分为几个部分一一对应
one

VCall(l:S,x:V,k:M): 代表l语句下调用x.k(..)Dispatch(o:O,k:M,m:M): 和之前一样的,找到对应函数mThisVar(m:M,this:V): 代表获取this变量Reachable(m:M): 代表添加可达方法mCallGraph(l:S,m:M): 代表l语句调用到函数m,正常的CG
1 | Oi∈ pt(x),m = Dispatch(Oi, k) ---> Oi∈ pt(M_this) |
即该条件转化为Datalog为
1 | VarPointsTo(this, o),Reachable(m),CallGraph(l, m) <-VCall(l, x, k),VarPointsTo(x, o),Dispatch(o, k, m),ThisVar(m, this). |
two

Argument(l:S,i:N,ai:V): 代表实参,即调用点的实参表示,调用点l的ai参数Parameter(m:M,i:N,pi:V): 代表函数中的形参,函数中的pi参数。
1 | Ou∈pt(aj),1≤j≤n ---> Ou∈pt(m_pj),1≤j≤n |
对应参数的传递,转化为Datalog即为
1 | VarPointsTo(pi,o) <- CallGraph(l,m),Argument(l, i,ai),Parameter(m,i,pi),VarPointsTo(ai,o). |
three

MethodReturn(m:M,ret:V): 代表返回值,即函数m中的返回值retCallReturn(l:S,r:V): 代表调用点l接收返回值到r
1 | Ov∈pt(m_ret) ---> Ov∈pt(r) |
对应返回值的传递,转化为Datalog即为
1 | VarPointsTo(r, o) <- CallGraph(l, m),MethodReturn(m, ret),VarPointsTo(ret, o),CallReturn(l, r). |
最终结果如下

实例
EDB

依据上述的例子能大概推导出相关的EDB了。
Rules
依据规则进行一一解析即可求得
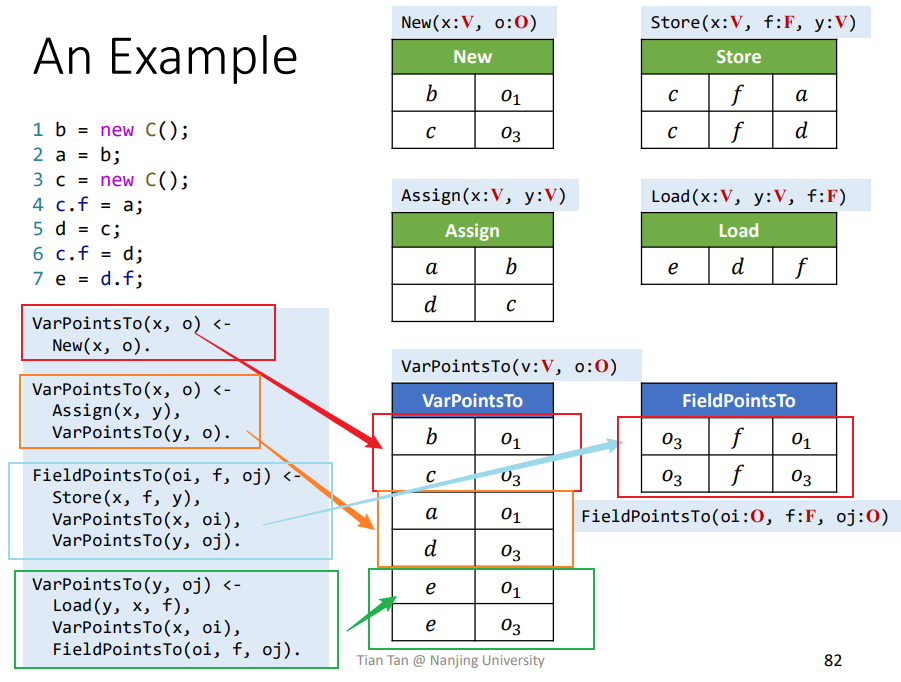
Whole-Program Pointer Analysis

处理New方法时,会限定在reachable方法中
4.Taint Analysis via Datalog
相关概念

主要是Taint(l:S,t:T)的解释,把所有的污点数据产生点call site,即l:S关联到产生的污点数据tainted data,即t:T。TaintFlow差不多是相同的。
source/sink

同样是一一对应的关系,即在指针分析中加入这个污点分析即可。
优缺点

优点Pros
比较整洁,容易实现,更容易基于现成的引擎优化进行改造
缺点Cons
因为Datalog的一些限制,导致其表达方式比较少,某些逻辑可能不能表达到位,比如一些for-all的情况等。此外Datalog因为大多基于一些引擎,导致其不能很好地控制性能。
总结

了解Datalog语言,学会通过Datalog实现指针分析、污点分析。
十四、CFL-Reachability and IFDS
1.Feasible and Realizable Paths
Infeasible Paths:
CFG中在程序运行起来并不执行的路径
Realizable Paths:
call和return相匹配的路径,即分析的时候不会依据函数传递到其他的变量,如下的调用点1和调用点2。
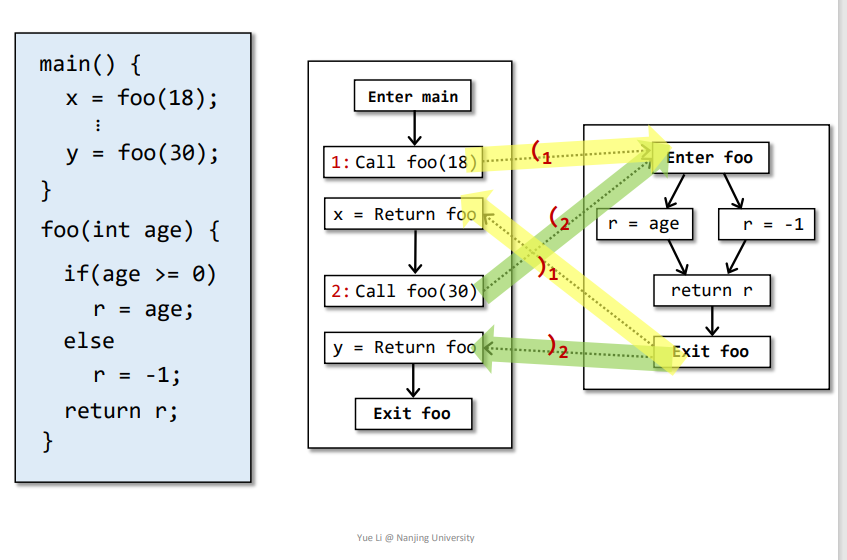
但是Readlizabale path其实也可能不被执行,因为可能该Readlizabale path的调用点是在Infeasible Paths中。另外unrealizable paths一定不会被执行。
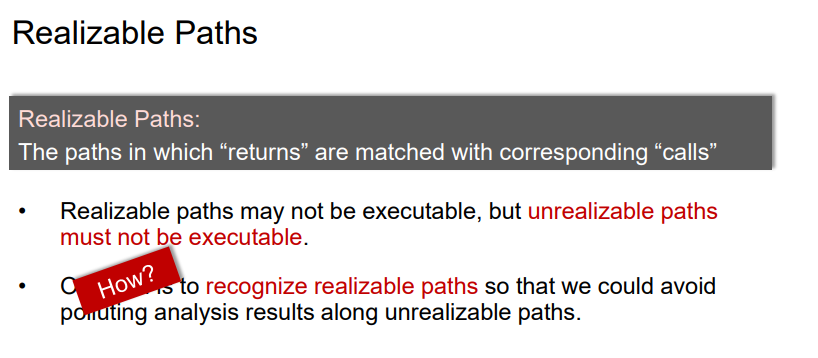
2.CFL-Reachability
一条A到B的路径中所有的边都有一个label,这个lable只能由确定的规则context-free language来定义

context-free language: 遵循context-free grammar(CFG)的语言context-free grammar(CFG):有点不理解,
Mark一下
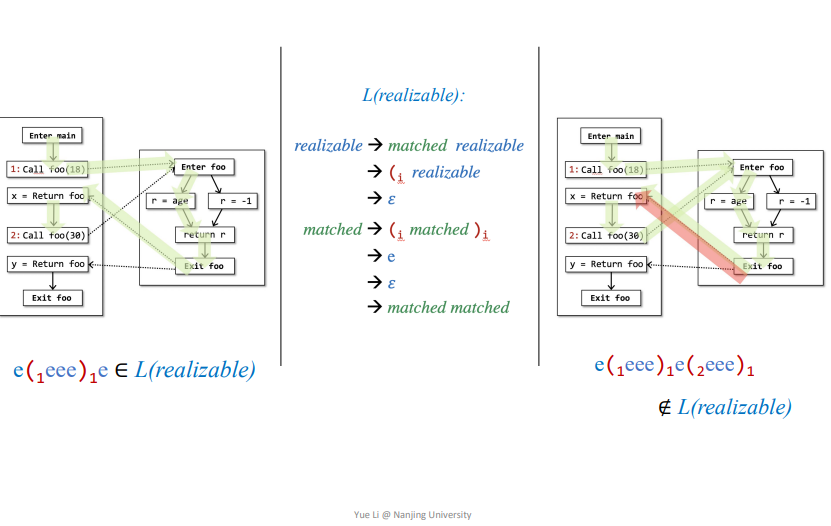
感觉就是一个加了标签的括号匹配算法,满足这个情况即是realizable
3.Overview of IFDS
概念

在过程间数据流分析中,如果一个f是可分配distributive,并且其domains是finite的,那么就可以用IFDS
Meet-Over-All-Realizable-Paths (MRP)
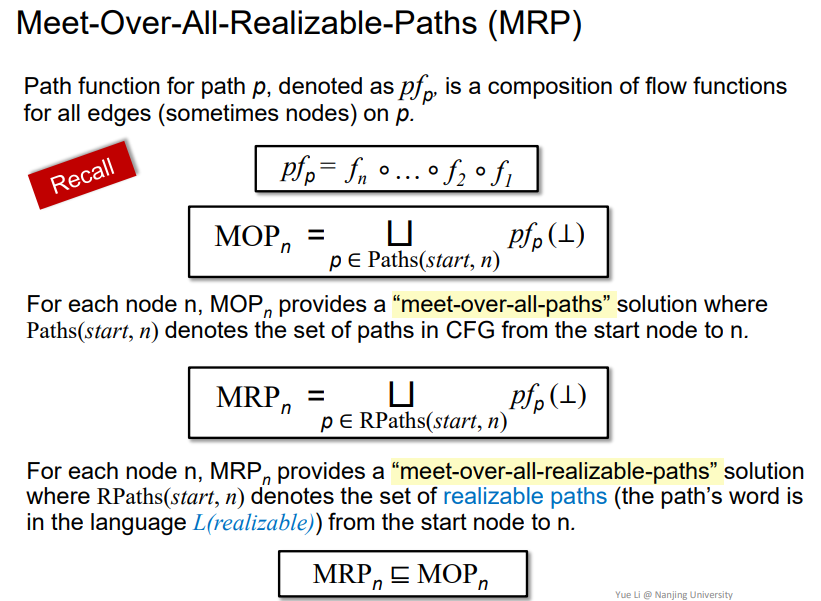
即在realizable paths上做MOP分析,更加准确
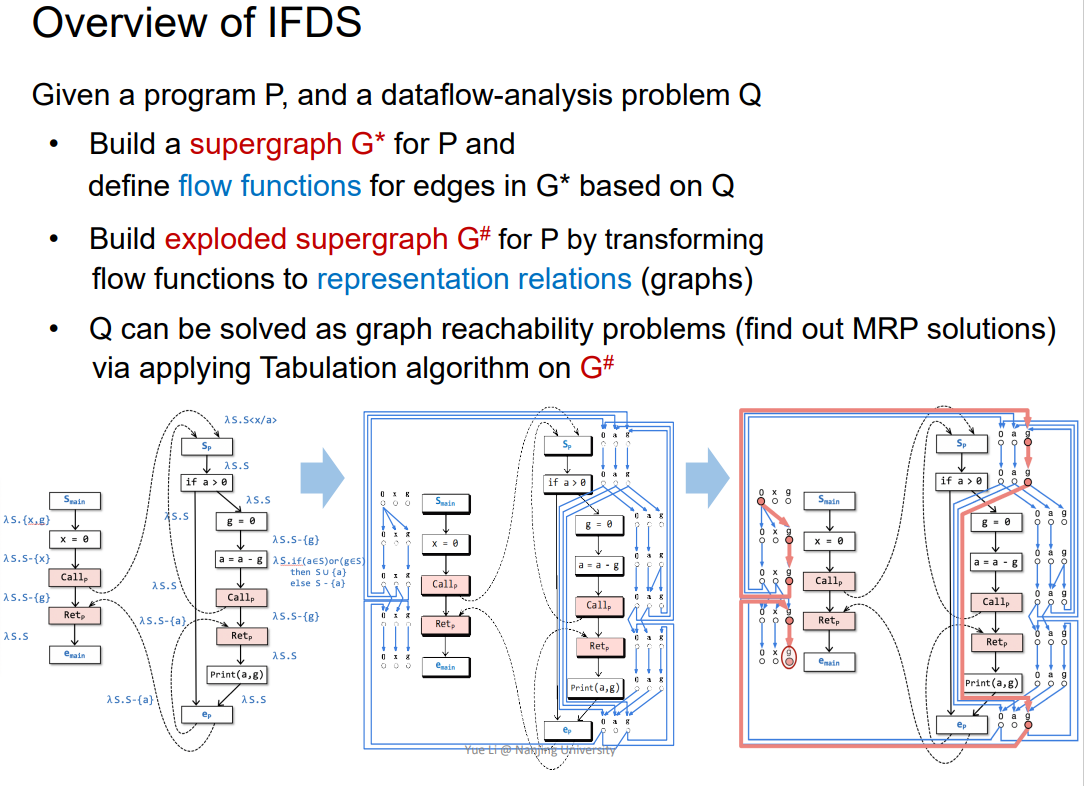
这里属实听得不太懂
Supergraph
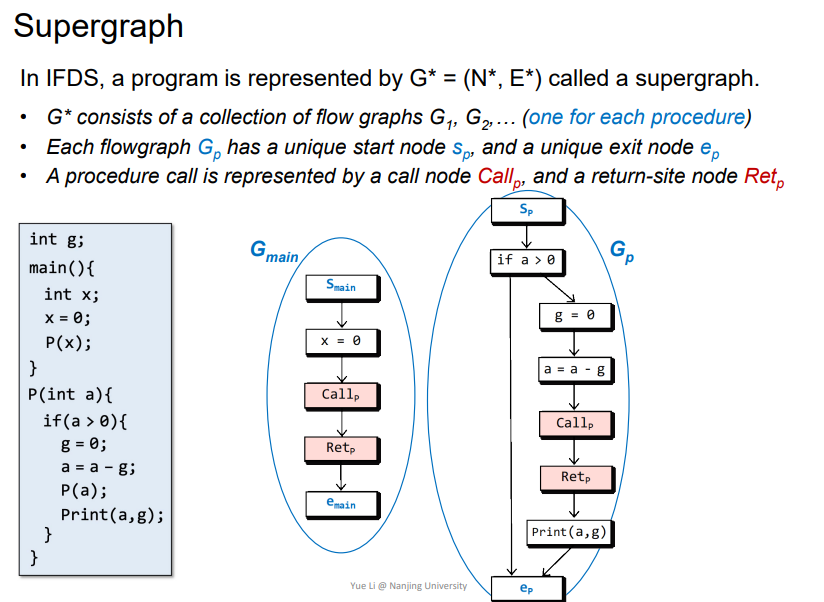
G* = (N* , E*): 即每个函数都有自己的FG(flowgraph),这里的例子即为G_main/G_p,而G_main加上G_p一起组成了整个程序的G*。- 每个函数的
FG中都会有s_p入口,以及e_p出口。此外对于函数调用的实现用call_p/ret_p来体现。
G*
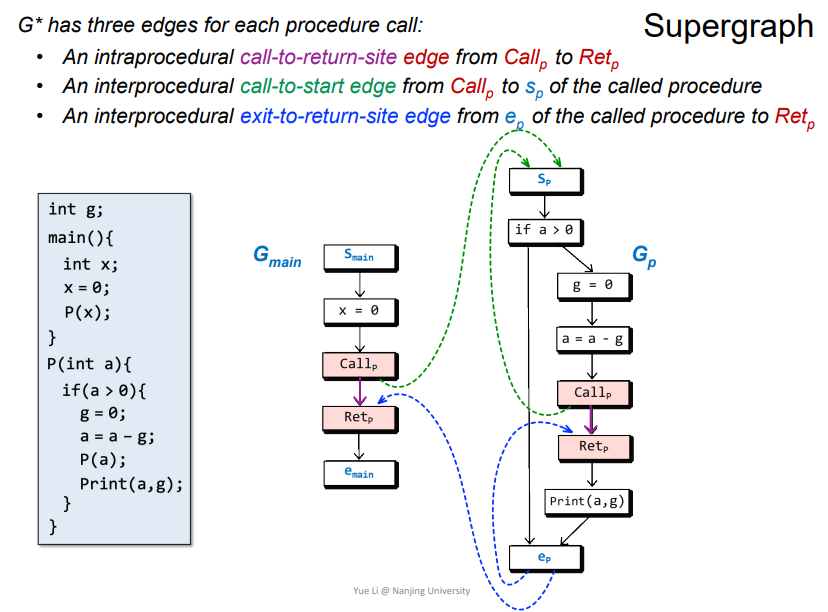
在每个程序调用中都有三种不同的边
call-to-return-site edge: 图中紫色的边,Call_p->Ret_P,在当前函数中。call-to-start edge: 图中绿色的边,Call_p->S_p,在不同函数中exit-to-return-site edge: 图中深蓝色的边,e_p->Ret_p,在函数返回时跳转到调用点
Design Flow Functions

N*: 程序中在没有实际运行前可能没有被初始化的变量λ e_param.e_body: 想想成一个匿名函数,λ为函数名,e_param为函数参数,e_body为函数体,相关的例子如上。
例子
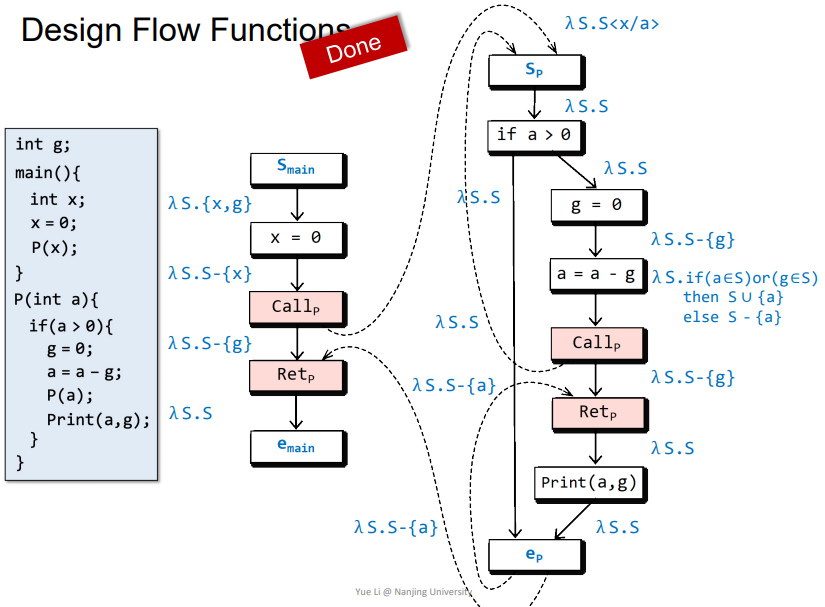
首先将未被初始化的变量加入集合
S:λ S.{x,g}x=0 -> Call_p: 代表x被初始化了,那么需要从集合s中减去x,即为λ S.S-{x}Call_p -> S_p: 发生了函数调用,相关参数的值发生传递,即将集合s中所有x替换成a,即为λ S.Sa=a-g -> Call_p: 当a或者g任意一个变量没有被初始化,那么a就没有被初始化,那么就将a并入到集合s,即为S ∪ {a}。反之,a/g都被初始化了,就代表a也会被初始化,那么就需要从集合s中减去a,即为S - {a}Call_p -> Ret_p:主要考虑两个情况
- 在函数中被初始化了,那么传回来的
S中就不会包含g,S-{g}也不包含g,两者相合不包含g,准确 - 在函数中没有被初始化,那么传回来的
S中包含g,S-{g}不包含g,两者相合包含g,准确
同样的如果不是
S-{g},那么情况如下- 在函数中被初始化了,那么传回来的
S中就不会包含g,S包含g,两者相合包含g,不准确 - 在函数中没有被初始化,那么传回来的
S中包含g,S包含g,两者相合包含g,准确
这样
S-{g}就会更加准确- 在函数中被初始化了,那么传回来的
e_p -> Ret_p: 发生了函数返回,需要减去本地变量,即为λ S.S-{a}
Exploded Supergraph
概念
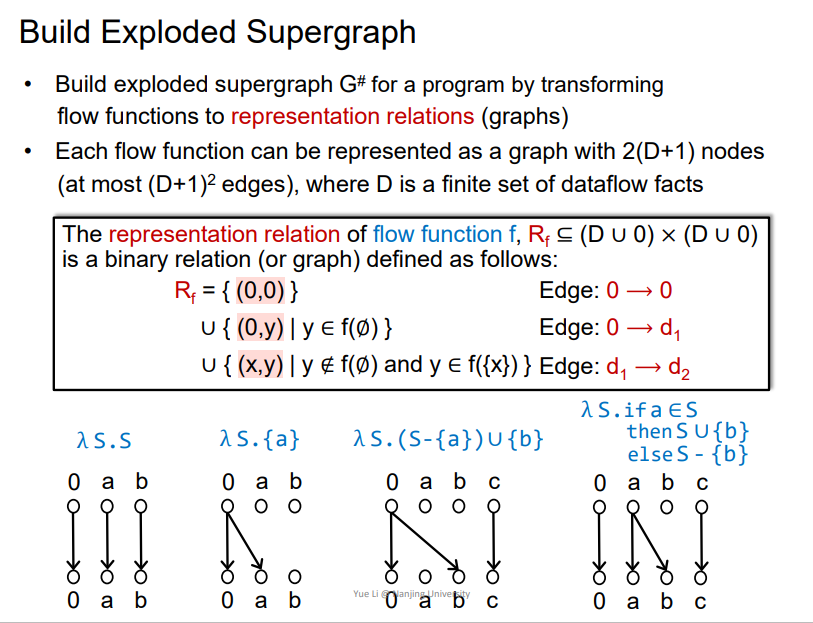
- 需要建立一个
representation relations (graphs) - 每一个
flow function都可以被表示成2(D+1)个节点的关系连边,D是dataflow facts的集合
Rule规则
0->0: 无条件存在0->x: 即无条件产生了xx->y: 即在有x的情况下,会产生y
大概依据上图可以判断一下

最终需要依据规则,将G*转化为G#
Why We Need Edge 0 ⟶ 0?
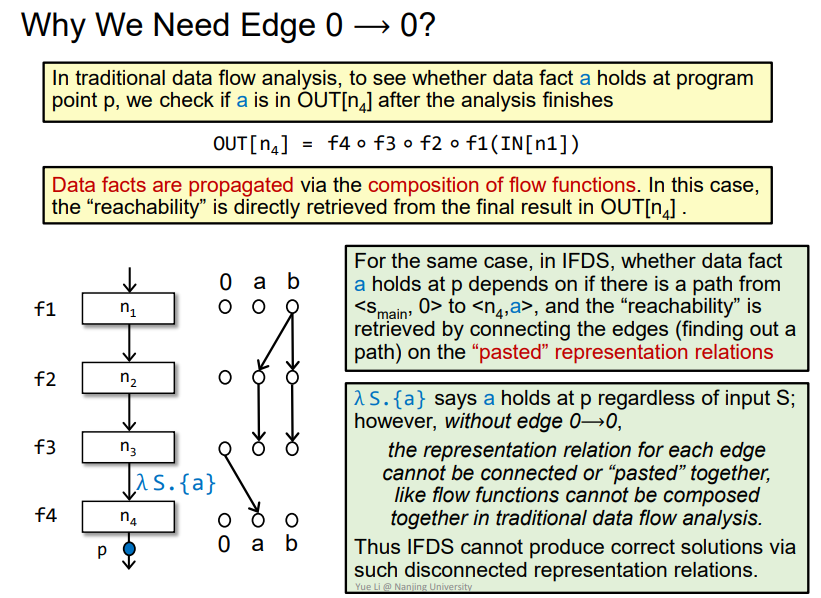
即需要0->0的边来在某点产生新的变量,使得传递reach成立,否则就没办法表达能够reach的概念,那么加入0->0如下
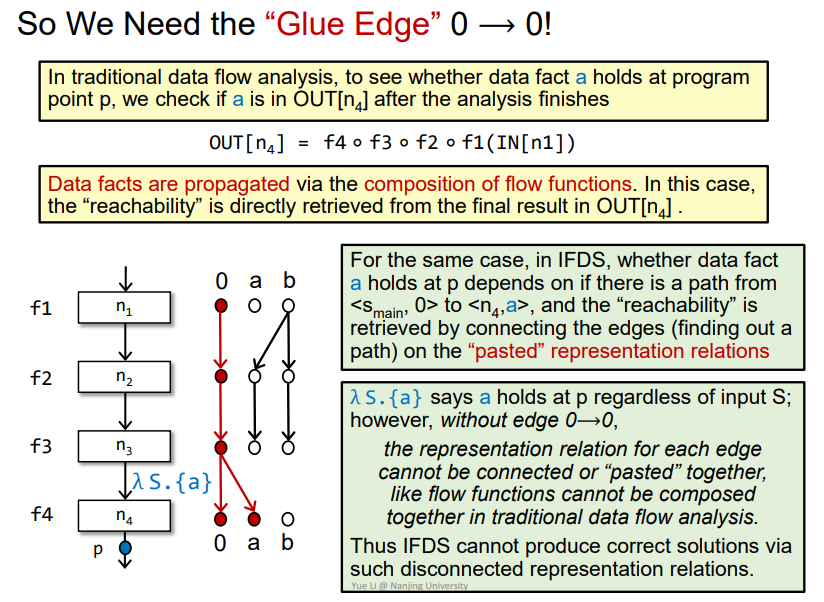
例子
依据相关规则得到如下结果
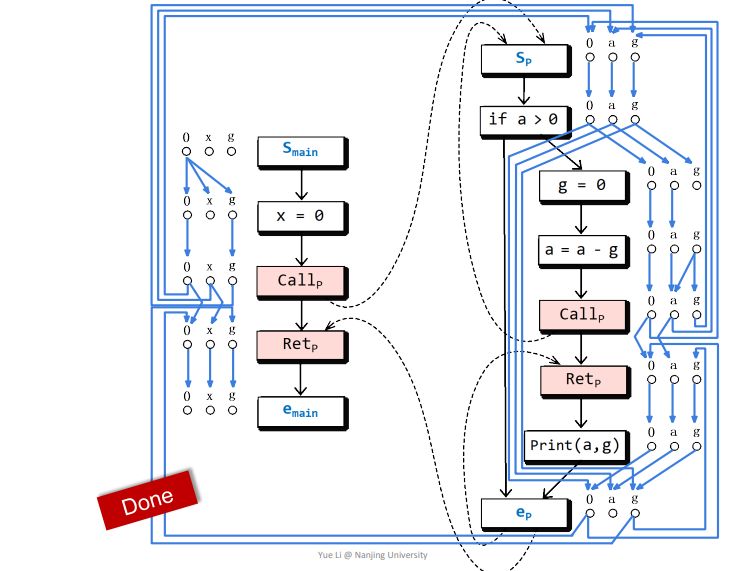
这个应该不难得到,通过这个图即可判断一些变量是否可达,比如下图画圈的g点就在realizable paths中可达
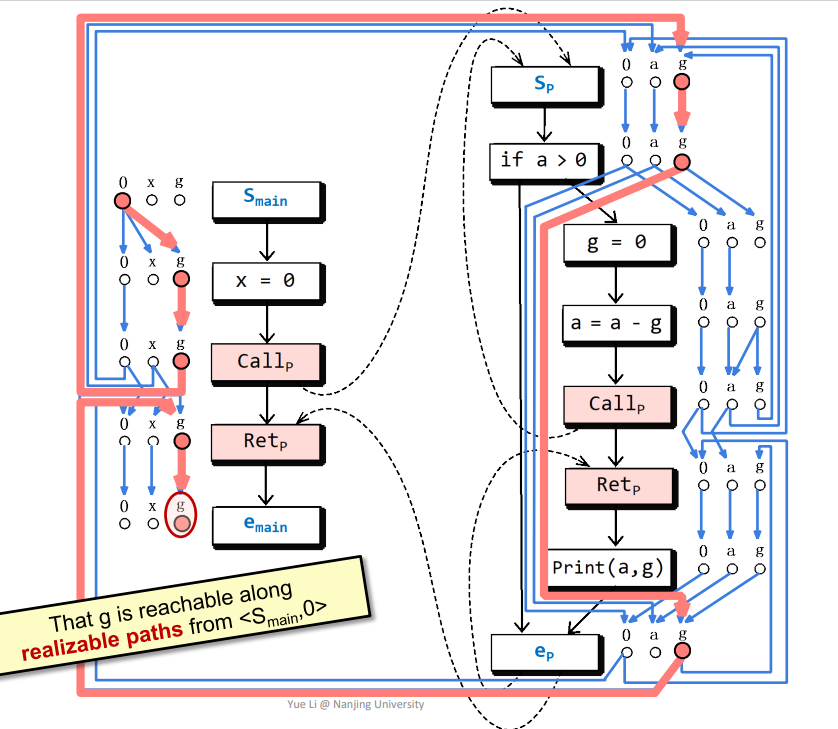
而下图画圈的g点只会在non-realizable paths中可达,因为该路径括号其实是不匹配的。

Tabulation Algorithm
依据G#,通过该算法寻找realizable paths寻找变量可达路径。该算法比较复杂,课程进行了简单介绍。具体算法如下

看到bsauce师傅写的真好:【课程笔记】南大软件分析课程11——CFL可达性&IFDS(课时15) - 知乎 (zhihu.com)
- 时间复杂度O(ED^3)
Core Working Mechanism of Tabulation Algorithm
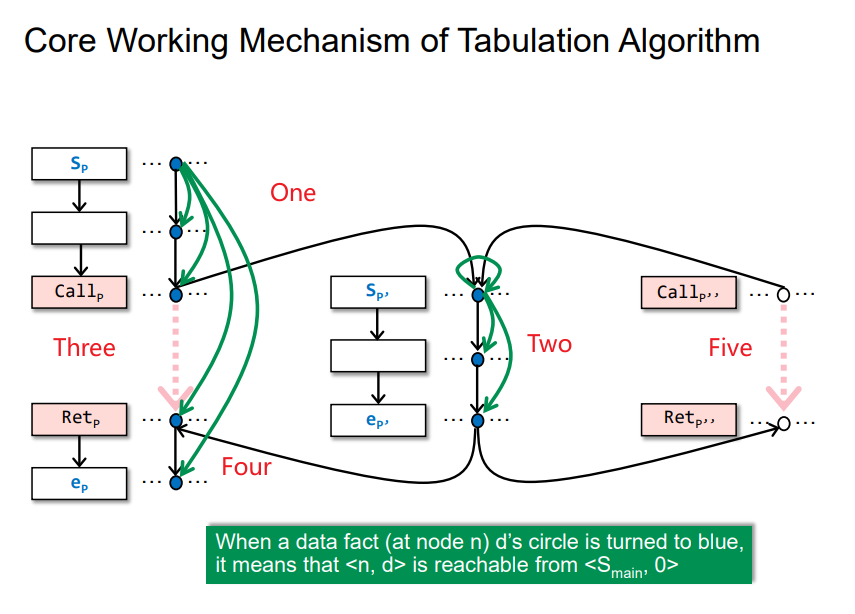
即依照给的顺序依次进行reach可达探测,但是完成Four之后,再碰到Five,就直接进行连边了,因为Two已经进行探测了,不需要再计算一遍了。
4.Understanding the Distributivity of IFDS
帮助判断该问题是否可用IFDS来解决

不可以用标准的IFDS来解决这两个问题
Distributivity
常见的分配律

Constant Propagation
但是对于Constant Propagation,该语句中的z的结果依赖于x/y共同的结果,并不能单独处理之后得到结果,无法满足分配律。这里其实就有点不懂了,比如之前提到的如下情况,不也是处理两个输入吗

有点不太理解,mark一下

- 当一个语句需要考虑多种输入数据才能得到正确结果时,就不是
distributive可分配的,不能用IFDS - 在
IFDS中,所有的数据以及传播都需可以被单独处理,这些单独处理并不会导致最终结果的正确性发生改变。 IFDS一次f只能处理一个data input
比如上述语句y = 2x + 3可以用IFDS来进行常量传播分析
Pointer Analysis
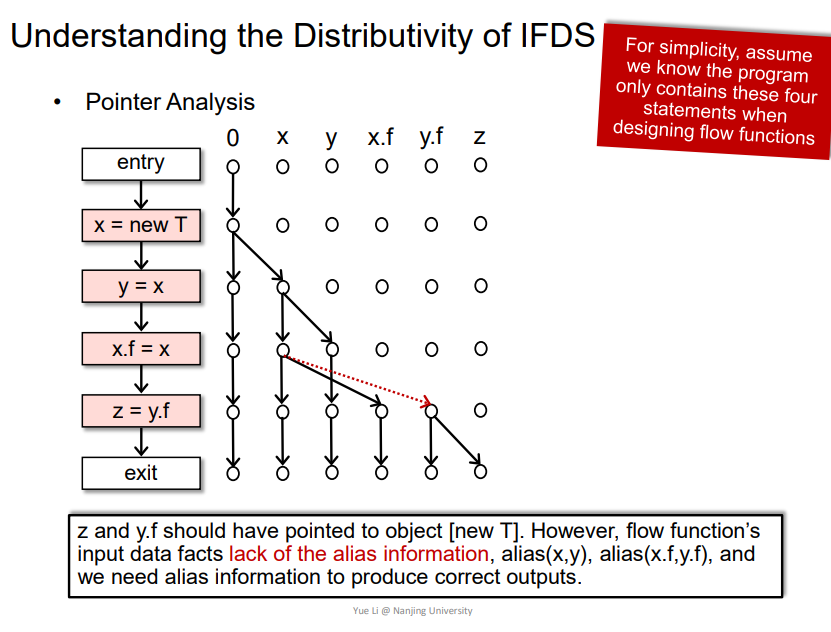
这个分析中,最开始分析没有图中红线部分,需要添加一个别名信息才可以alias,即y=x这个情况,但是需要别名信息的话,又要处理多个输入x/y,所以不能用IFDS
总结

理解CFL-Reachability(括号匹配问题),基础的IFDS,以及什么问题可以用IFDS进行解决
十五、Soundness and Soundiness
1.Soundness and Soundiness
Soundness

可以分析程序所有可能的执行结果,包括动态运行的,称为Sound。但是无论学术界还是工业界中,基本都是UnSound,即无法分析到程序所有可能的执行结果。
Hard Language Features for Static Analysis

即一些比较难以进行程序分析的语言。
有的分析研究希望能够寻找到一个保守估计的结果进行分析,比如C/C++里面的Point的地址进行加减的时候,就将该整个块当作指针可能的结果进行分析,但是也会相当不准确。

大部分的研究说分析是Sound的,其实都不是Sound,这些都会造成一些误导,导致过分依赖这个分析。
Soundiness
2015年是一些学者出来呼吁说程序分析的研究要标注Soundiness。即在发表的研究结果中,某些难以分析的部分需要充分说明,并且标注Soundy,表示告诉读者这部分在努力实现Sound,但是也不一定能够达到Sound。

对比

Sound: 比较理想化,能够处理程序所有可能的运行结果Soundy: 企图处理程序所有可能的运行结果,但在hard language features可以是unsound的,进行大概处理。Unsound: 为了相关的精度、效率等故意不处理某些部分。
2.Hard Language Feature: Java Reflection

对于程序分析而言,JAVA reflection使得分析JAVA变得很困难

Java Reflection
这个可以参考一下p神讲的
GitHub - phith0n/JavaThings: Share Things Related to Java - Java安全漫谈笔记相关内容

即利用反射相关API来获取JAVA中类,然后通过类创建对象,获取属性,修改属性等,这里讲得听清楚的。
Why We Need to Analyze Java Reflection?
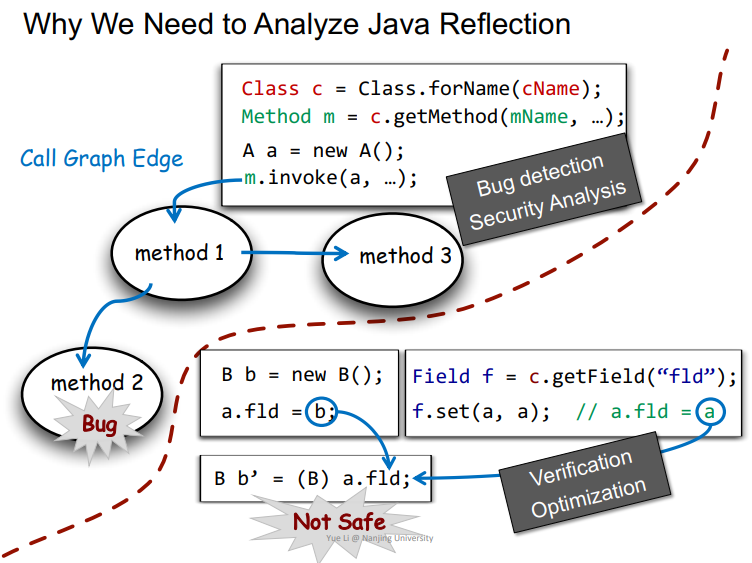
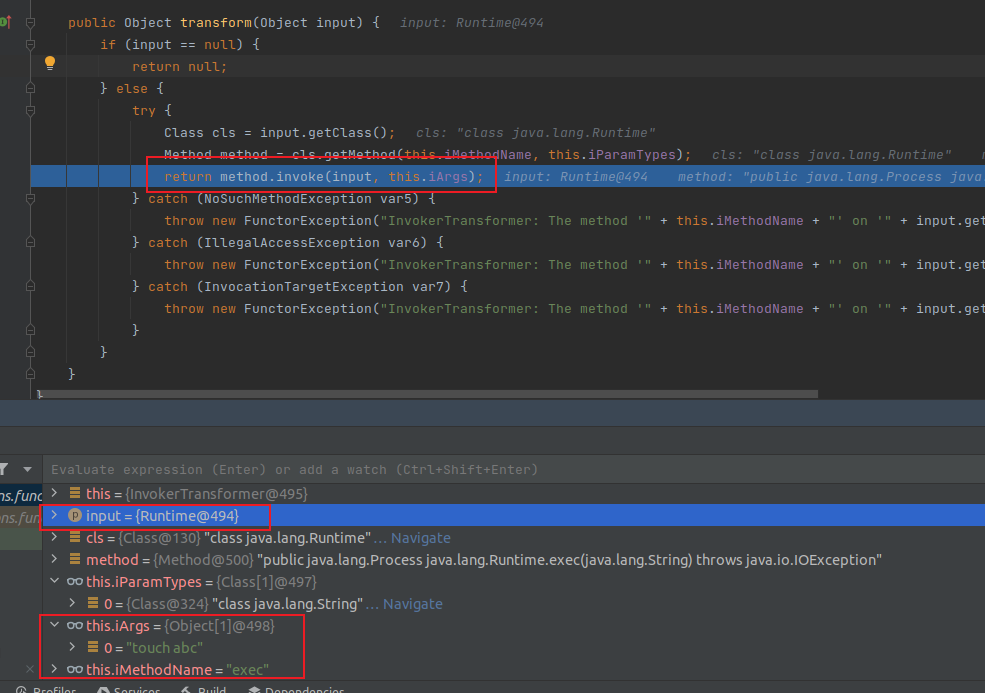
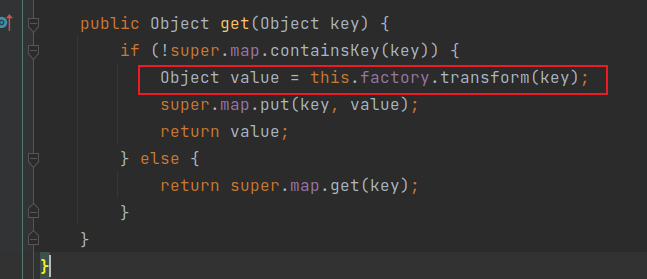
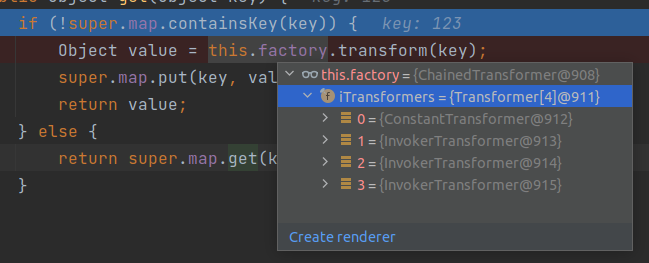
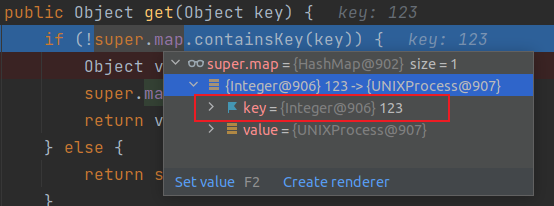
依据之前学到的指针分析,其实在分析的时候,不一定能检测出来该指针指向的是哪个对象,也可能分析出来指向多个对象。那么当调用到m.invoke这种反射里面常见的API时,由于m解析不正确,那么就会导致m.invoke没办法正常调用,就会出现bug。
或者在另一个例子中,两条流向会使得a.fld指向两个对象,那么就会导致B b’ = (B) a.fld;的cast发生错误。
How to Analyze Java Reflection?

String Constant Analysis/Pointer Analysis
从05年开始出现一种方法。

如果在反射中,相关的字符串通过String Constant Analysis可以求得,那么即可进行相关解析。但是如果没办法求得的时候,比如旁边黄色框列出来的部分,就没办法进行反射解析了。
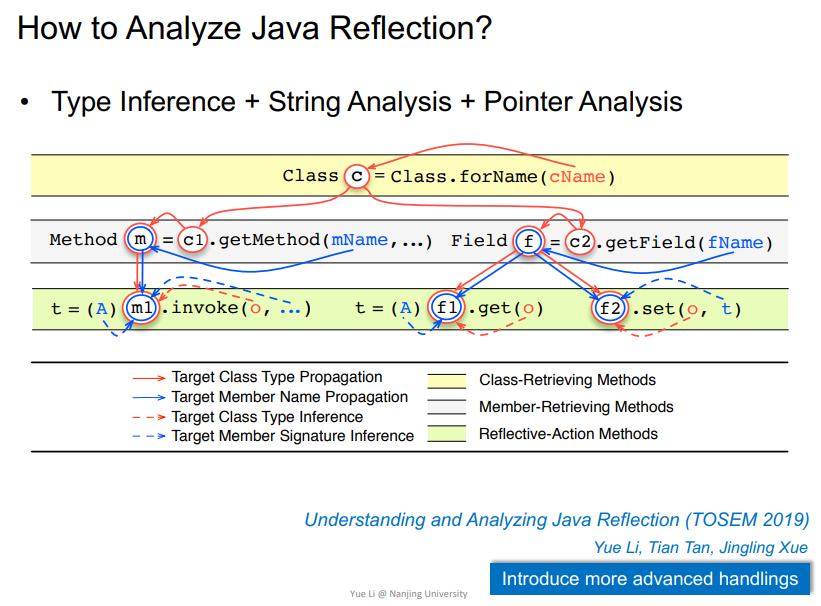
Type Inference/String analysis/Pointer Analysis
14年出现另一个方法,即老师们提出的

概括如下

即使用该反射的时候可进行解析

在该例子中,由于函数名是_加上CMD确定的,所以无法准确解析到对应的函数。
观察函数调用点175行,可以看到其parameters是个Object[]数组,那么这里创建的Object[]数组其类型必定在JAVA导入包中某些类,比如这里的FrameworkCommandInterpreter,是其sub/supertypes子类或者父类。
依据这个信息,在JAVA类型系统中寻找匹配相关的函数,会找出来很多函数,在该例子中,有50个函数被找到,其中48个函数都是可能会被调用的,即true。
这方面的最新研究也是老师们的研究最前沿
求解到的反射对象更准确更多,并且可以说出哪里解的不准。
Assisted by Dynamic Analysis

利用动态分析来求解,比如上面的cmd,将之用一个模糊用例进行动态执行,类似现今很流行的模糊测试,当匹配用例上证明就可能会调用到。
优点是求解出来的一定是准确的,因为必定是可能调用到的。
缺点就是常见的模糊测试的缺点,覆盖路径有限,比较慢。
3.Hard Language Feature: Native Code
Native Code
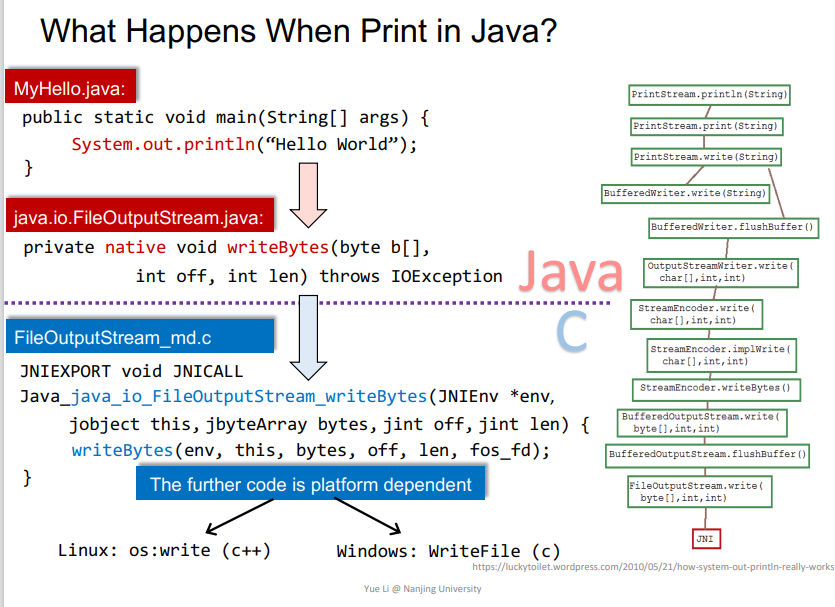
JAVA代码从头往下的相关函数调用,其中相关的动态链接库中的代码就是Native Code,用IDA打开即为相关的汇编代码,可以直接运行在对应的操作系统CPU上的。但是在下面的分析中,还是看它的源代码形式,比如C/C++形式。
Java Native Interface (JNI)
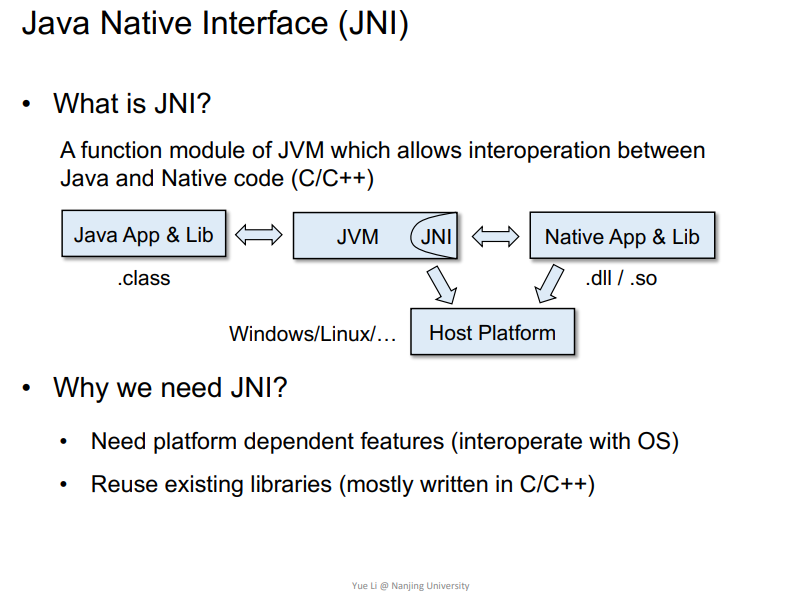
用来和相关动态链接库进行交互的编程框架,比如JAVA就可以调用到C/C++编写的动态链接库,即为JNI框架
Why Native Code is Hard to Analyze?
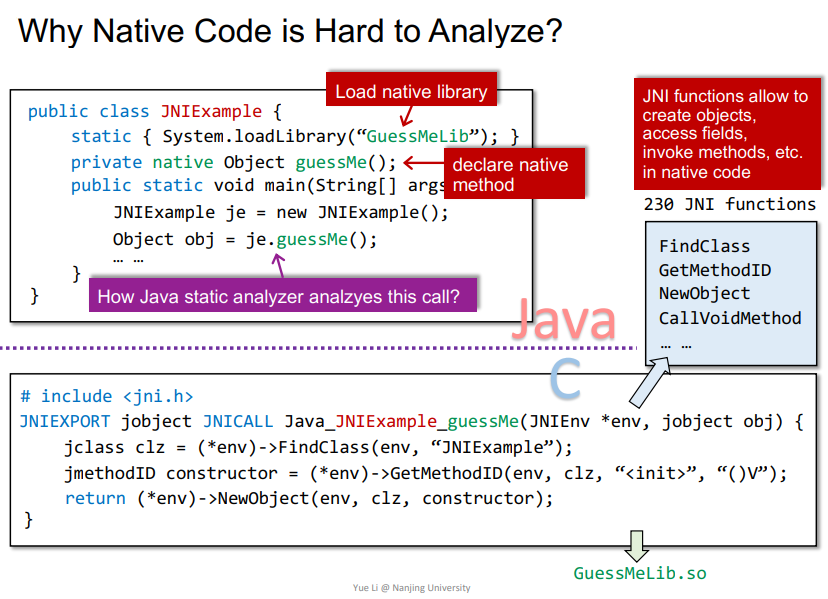
在JNI例子中,首先加载动态链接库,声明函数。其中*env变量用来传递JAVA中相关的一些信息,可以在Native Code中创建对象、属性、调用JAVA中的方法等。主要问题是跨语言之后,如何静态分析je.guessMe()这个调用?
参考:【课程笔记】南大软件分析课程12——Soundiness(课时16) - 简书 (jianshu.com)
因为Native Code是在库里面了,其源代码基本没有,只有一个接口库文件.so/.dll,那么就比较难进行分析了。
How to Handle Native Code?

手动建模分析
Native Code Modeling (Example)

直接将对应的函数简化成JAVA代码来进行分析,相当于hook掉相关的API,然后用类似功能的JAVA代码来替换掉。
前沿

前沿的一些分析,此外可以参考http://soundiness.org进行深入研究。
总结

理解Soundiness的大概概念,以及JAVA反射机制和Native Code为什么比较难分析。











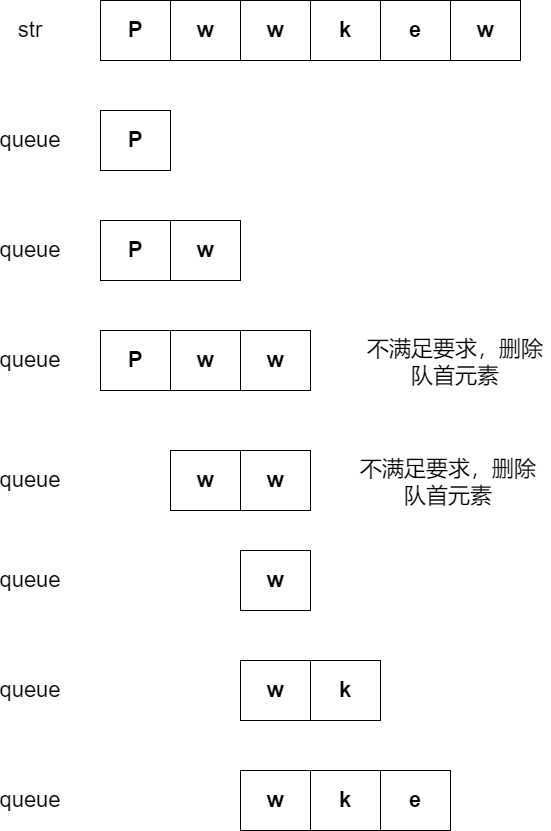

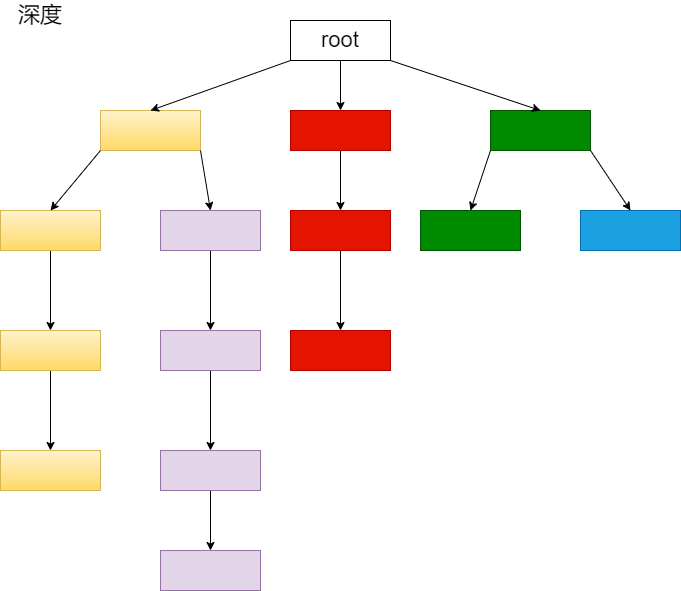
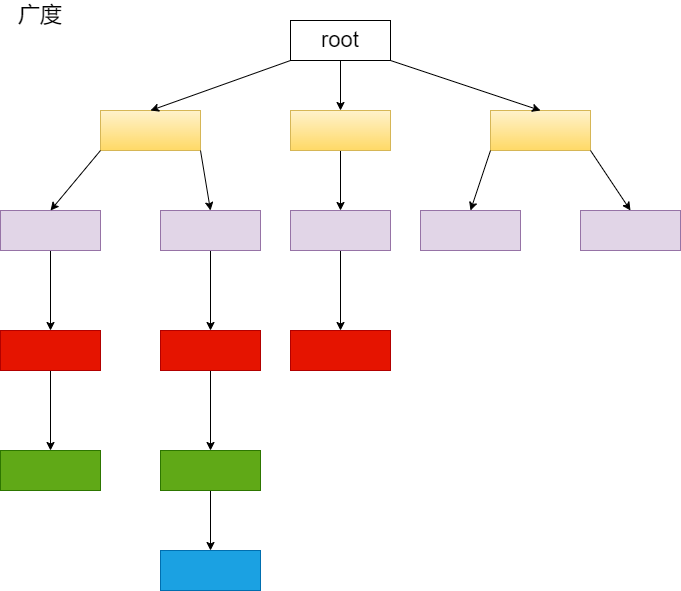
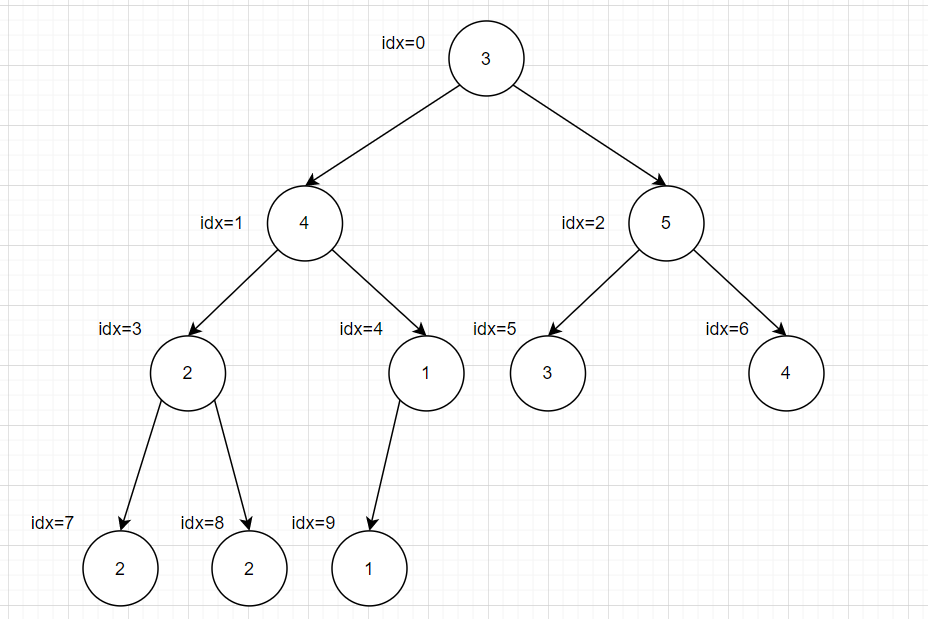
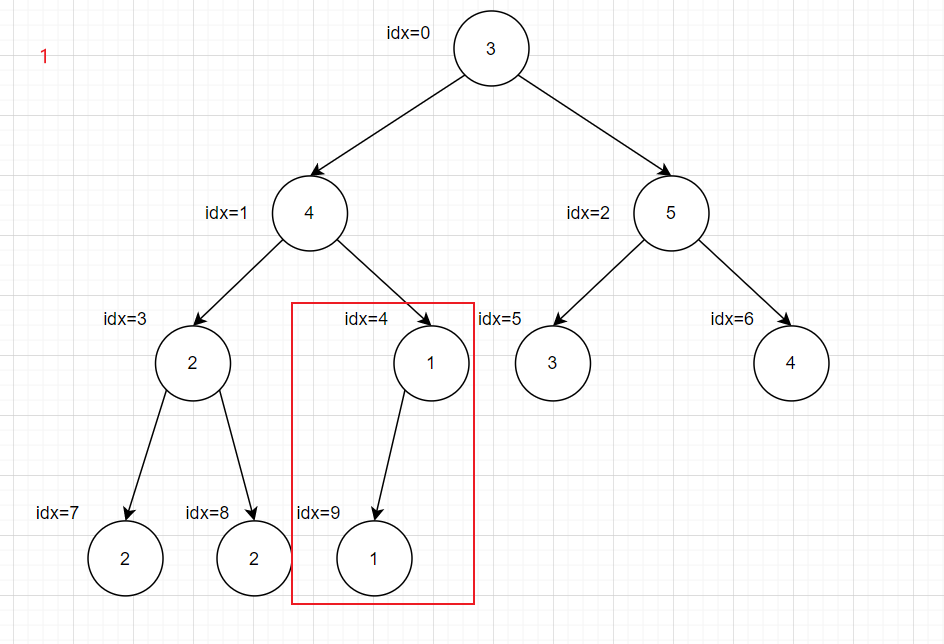
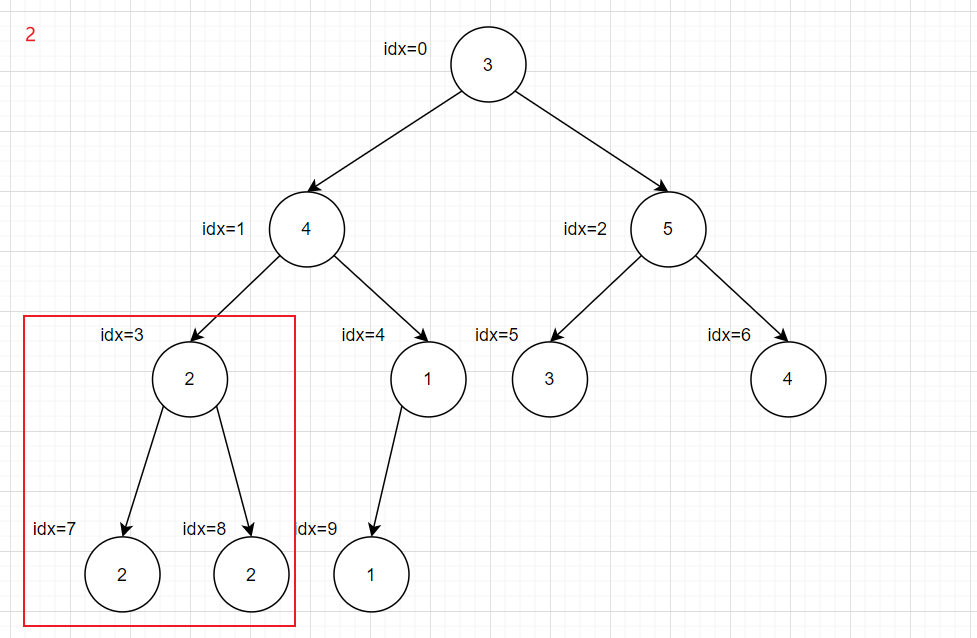
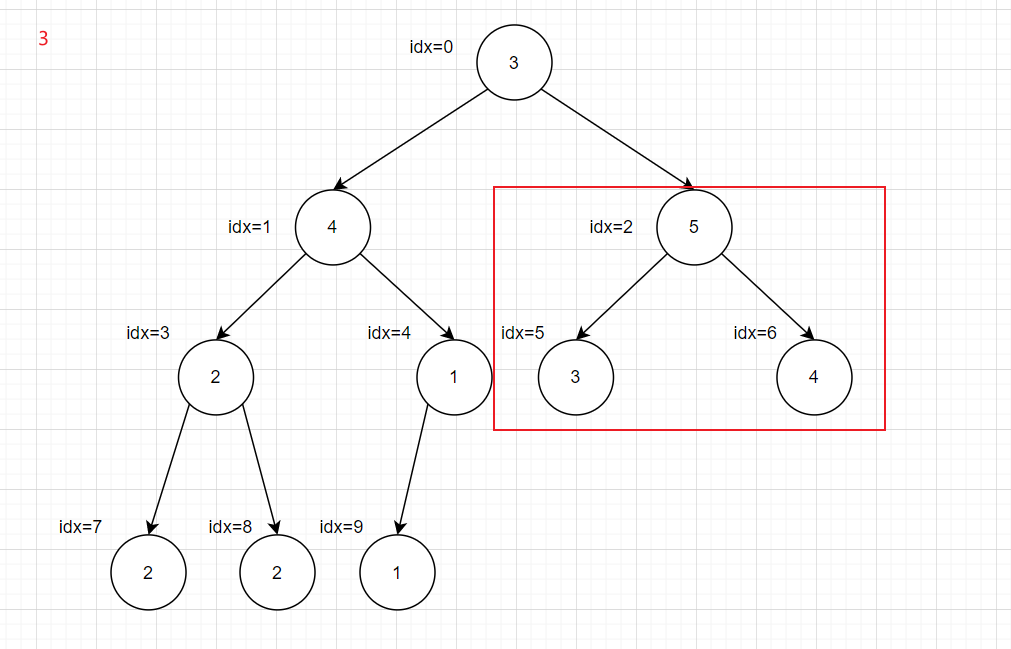
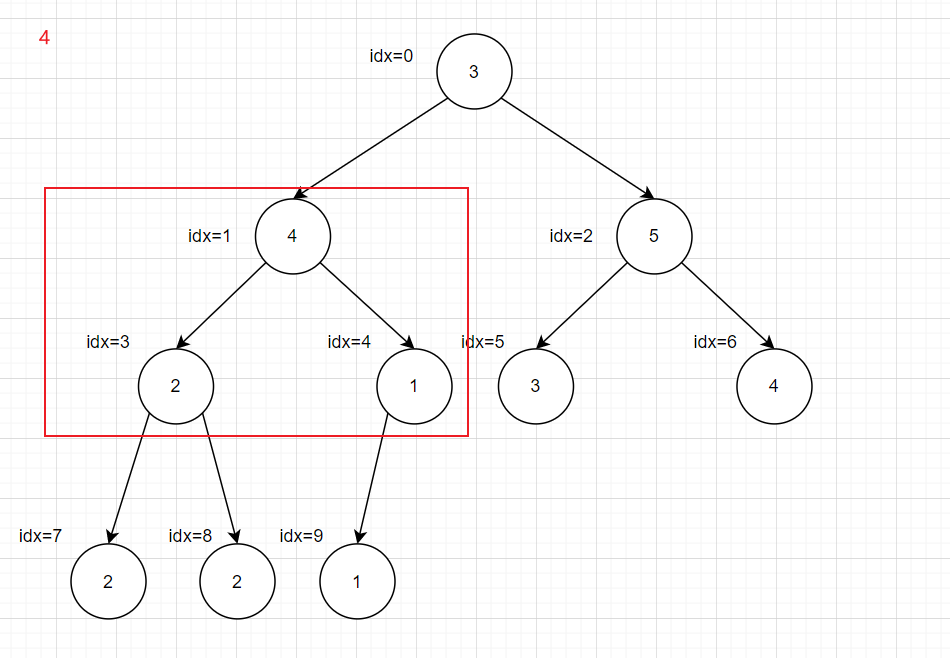
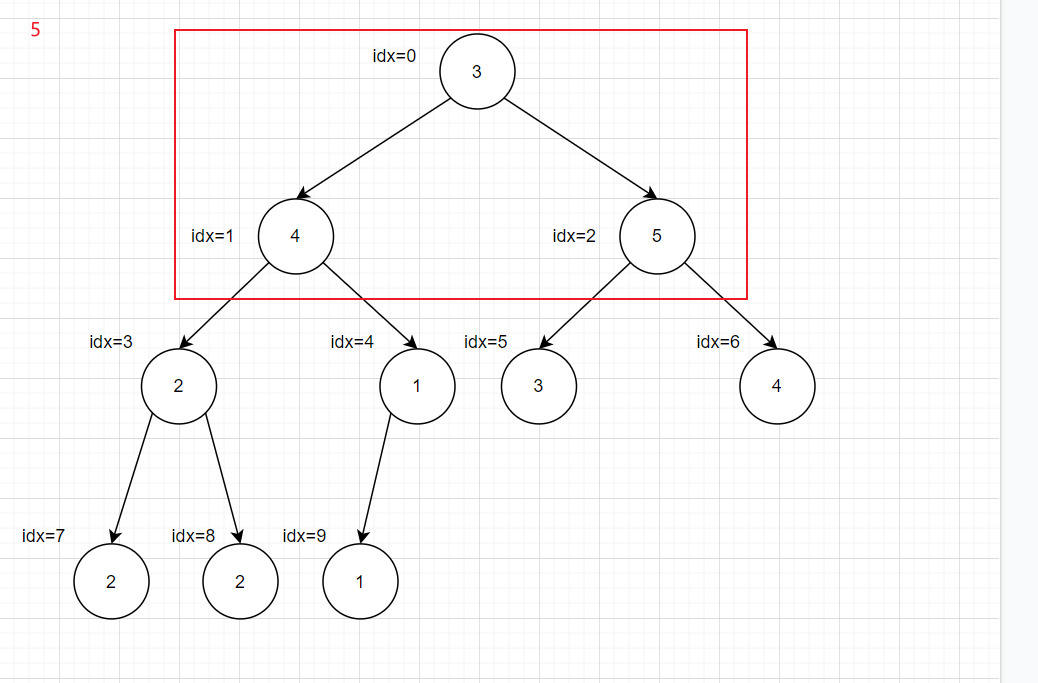
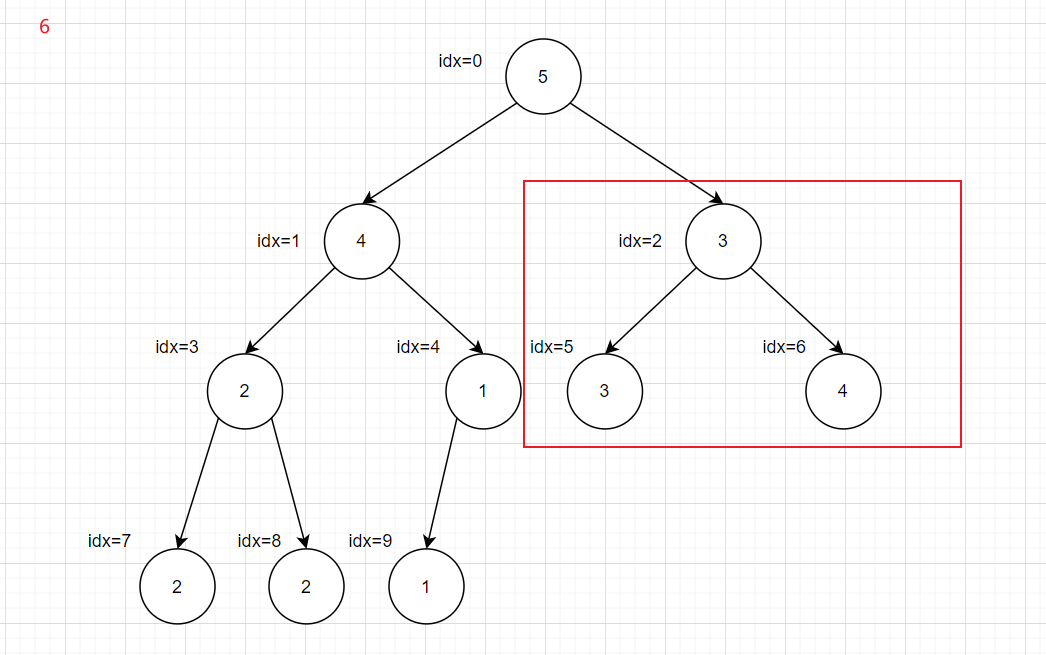
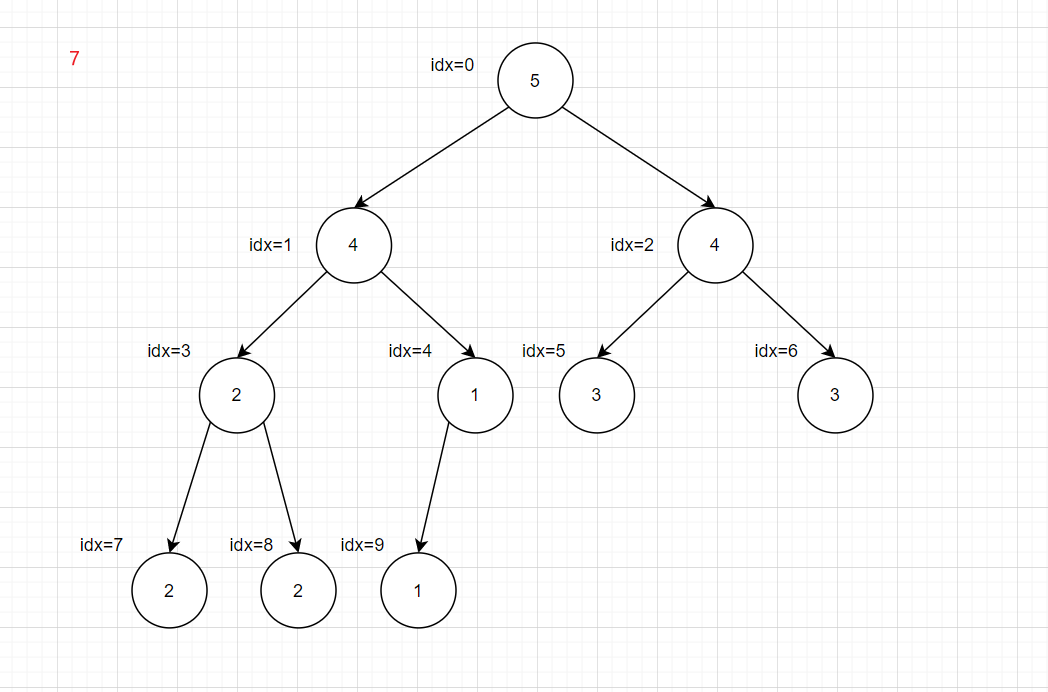



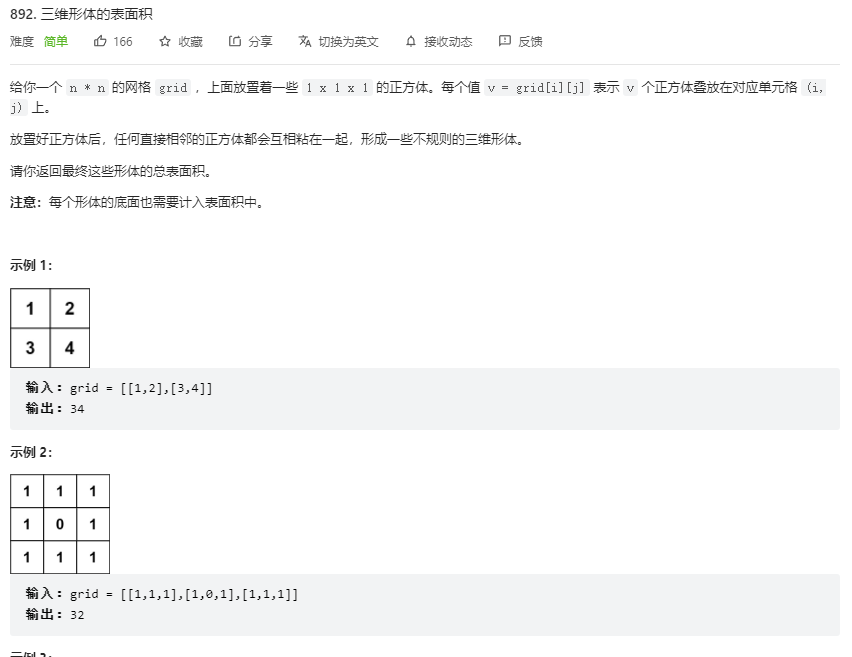

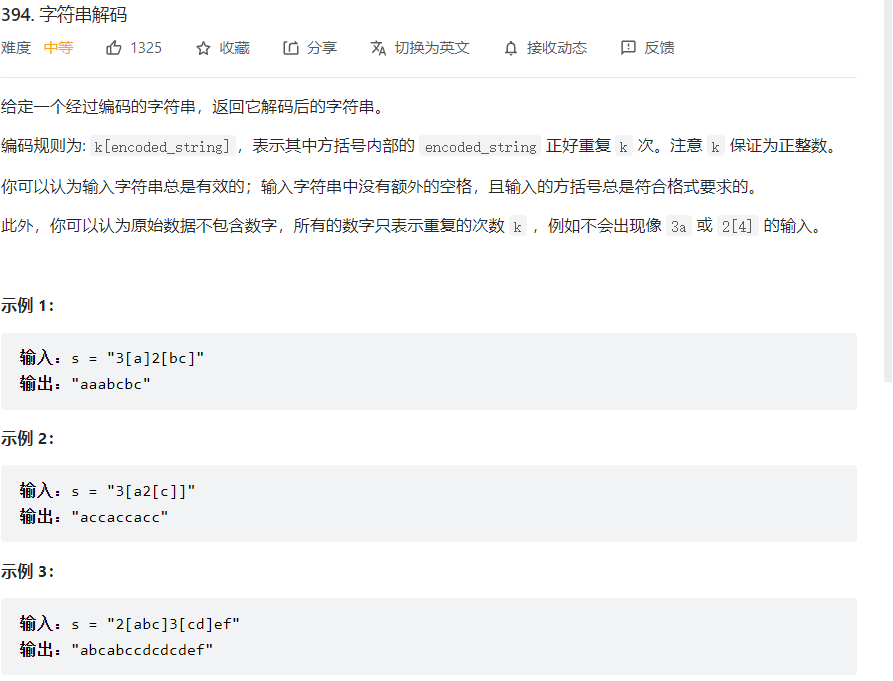
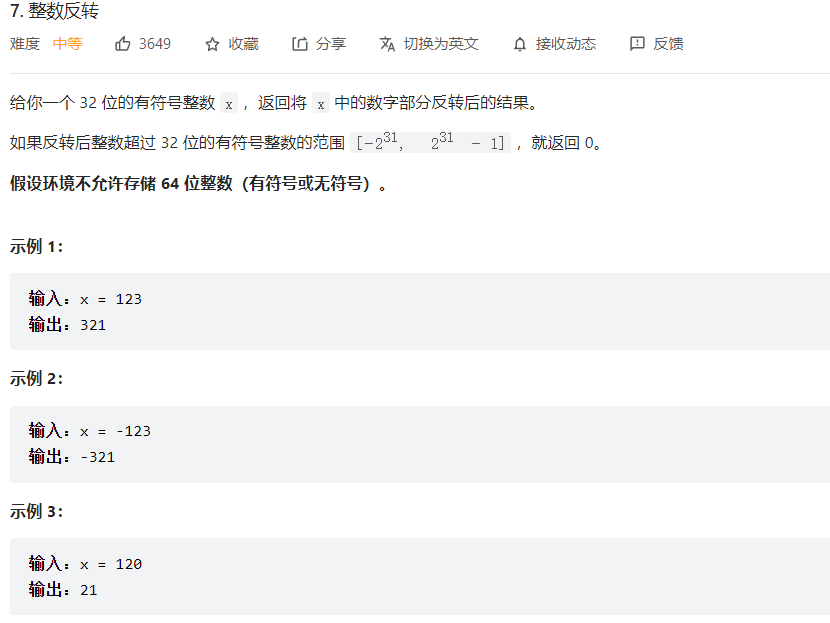
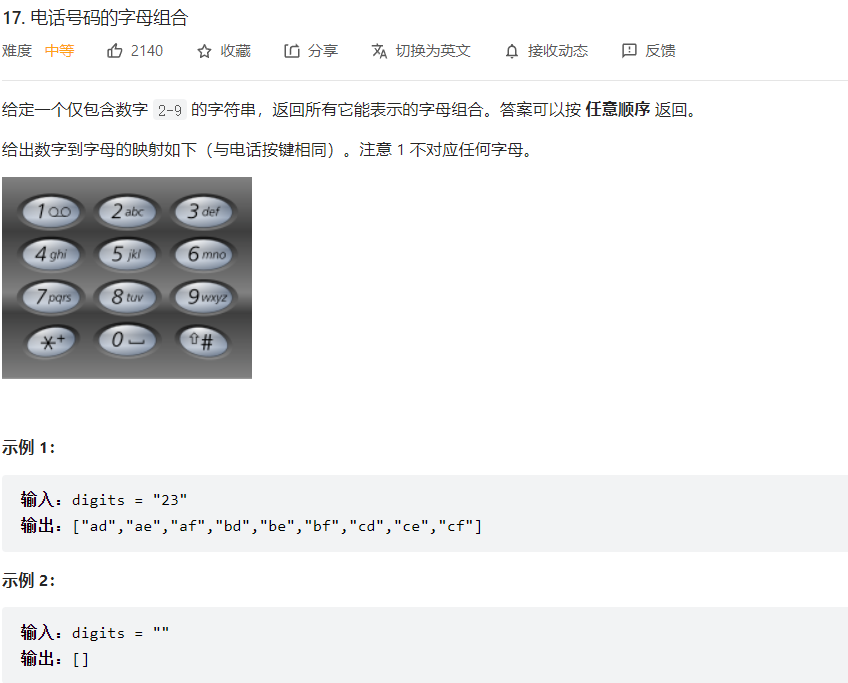
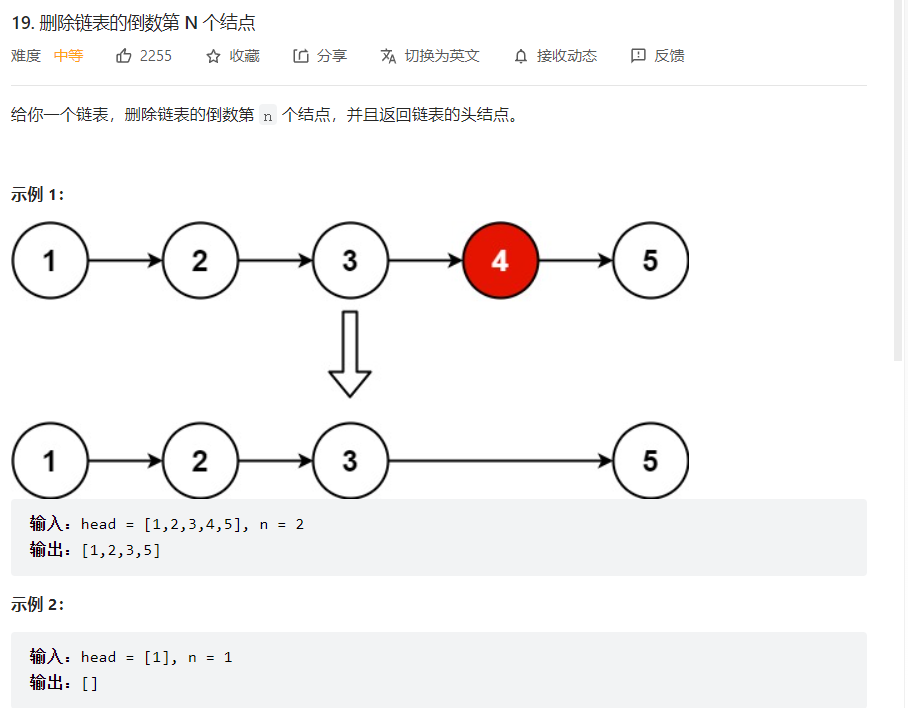
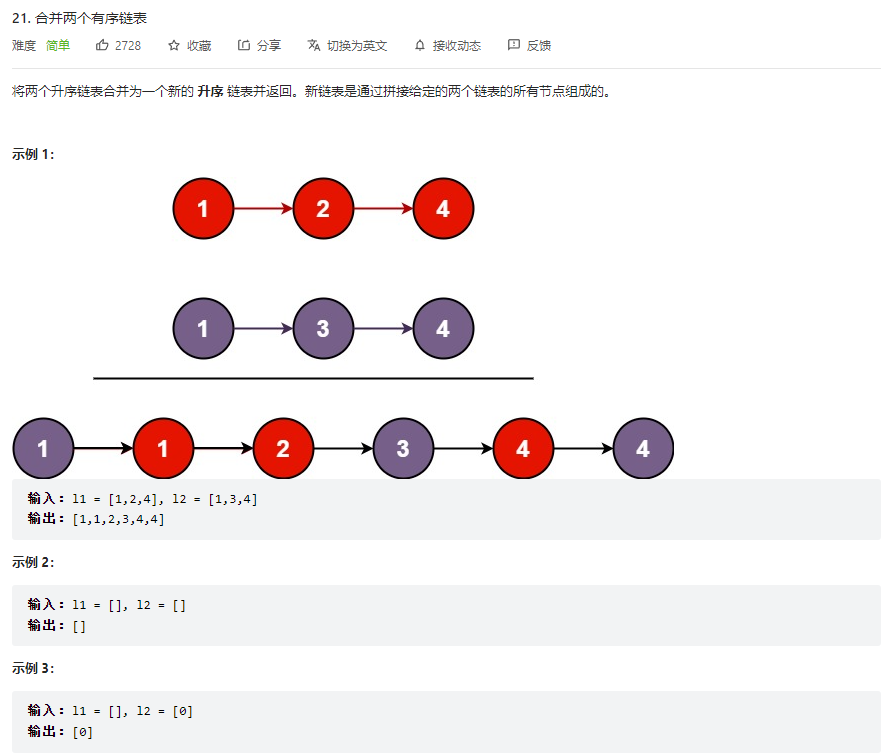
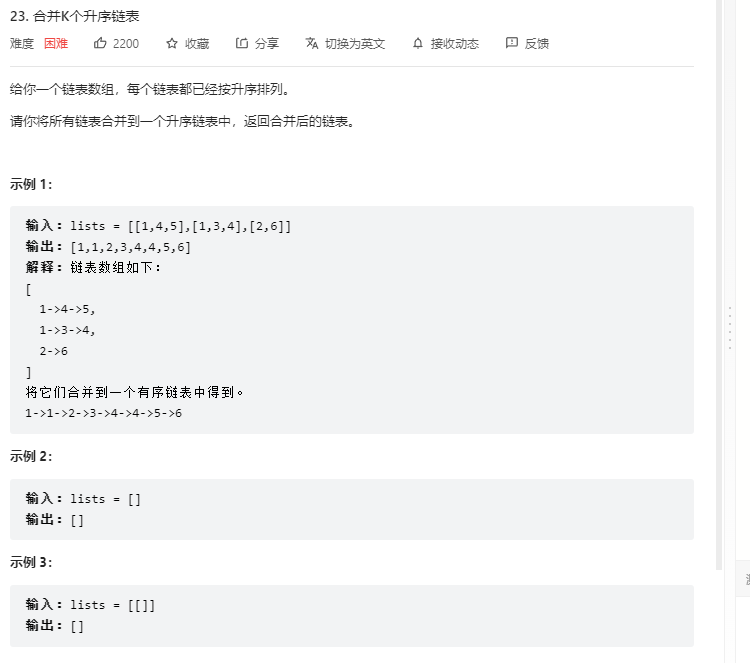

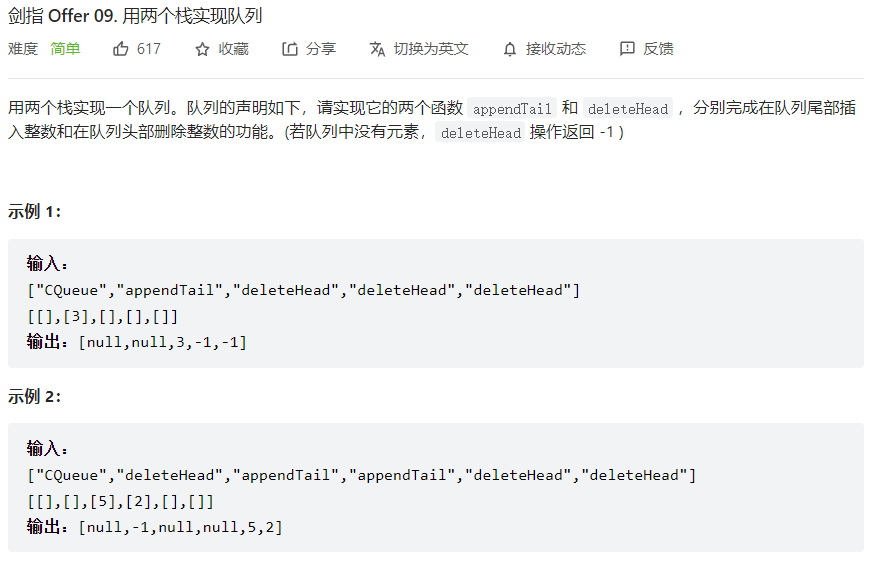
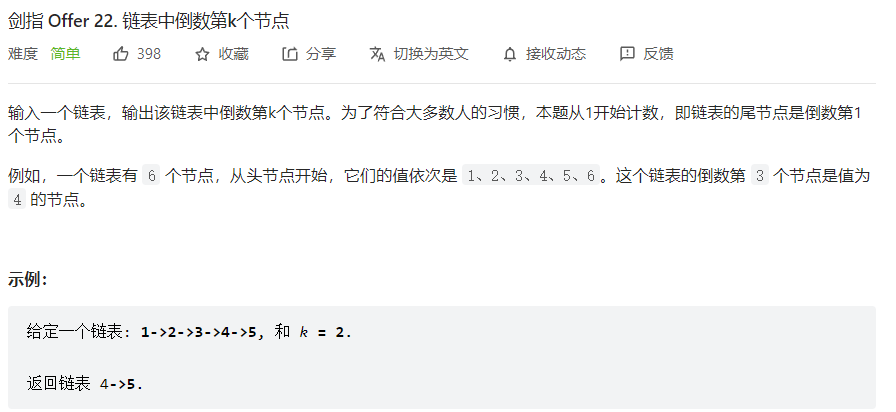
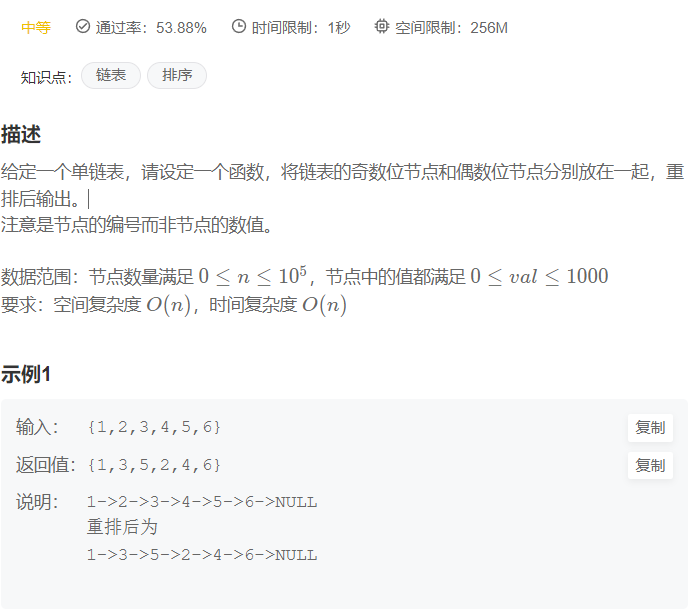
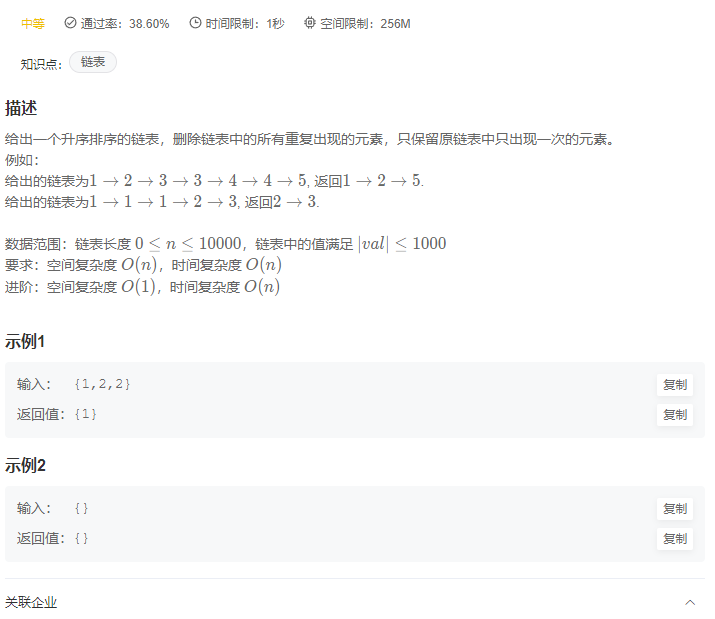
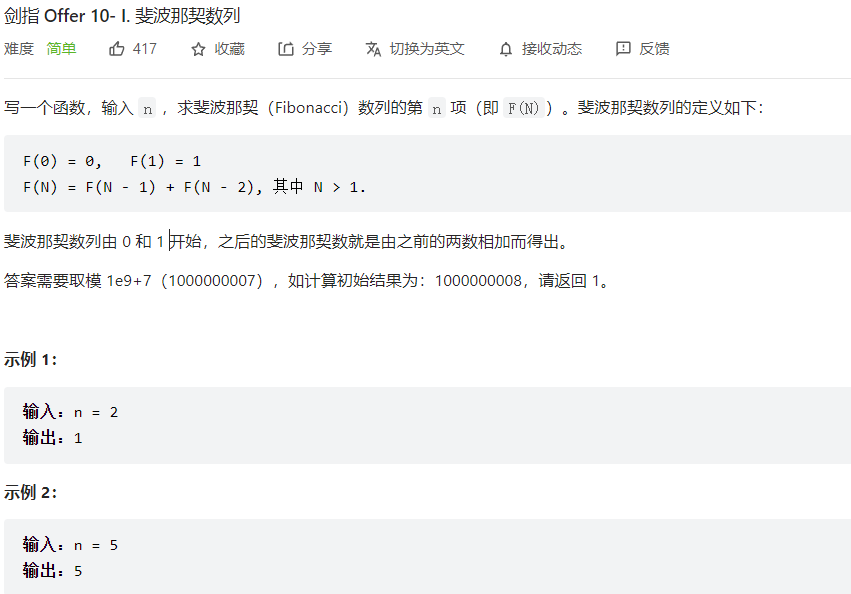 递归会超时,所以转化为循环
递归会超时,所以转化为循环